Sinusrelationerne i stumpvinklede trekanter

Man skal være varsom med at bruge sinusrelationerne i stumpvinklede trekanter.

Hvis vi får at vide, at vi har en trekant ABC, hvor A=22º, a=5 og c=10 og bliver bedt om at finde vinkel C, så ville vi normalt bruge sinusrelationerne.

$$\frac{\sin C}{c}=\frac{\sin A}{a}$$

$$\sin C=\frac{c\cdot\sin A}{a}$$

$$\sin C=\frac{10\cdot\sin(22)}{5}\approx0,75$$

$$C=\sin^{-1}(0,75)=48,5^\circ$$

Vi får altså, at vinkel C er 48,5 grader, hvilket er mindre end 90, så vinkel C er spids. Imidlertid kan man konstruere en trekant, hvor A=22º, a=5 og c=10, men hvor vinkel C er stump. 

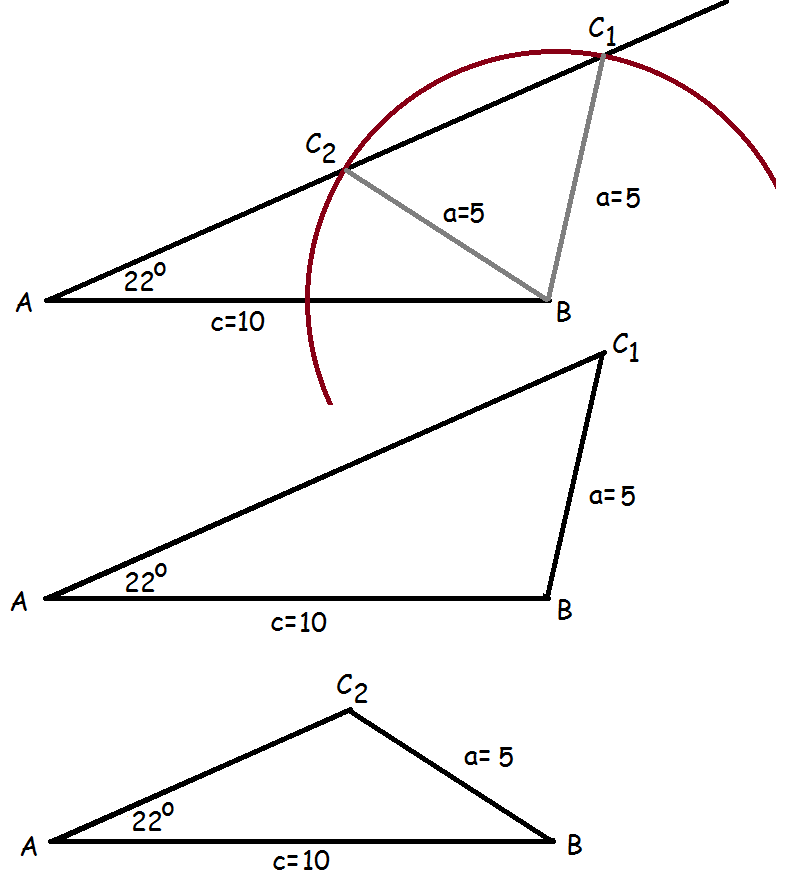
Vi kan altså konstruere to forskellige trekanter, der opfylder de givne oplysninger: En hvor vinkel C er spids, og en hvor den er stump. Når vi bruger sinusrelationerne, finder vi altid frem til den spidse vinkel.

Men heldigvis findes der er sammenhæng mellem vinklerne C₁ og C₂
Der gælder nemlig at

$$C_1=180^\circ-C_2\quad\Leftrightarrow\quad C_2=180^\circ-C_1$$

Hvis vores opgave i stedet havde lydt I trekanten ABC er A=22º, a=5, c=10, og der oplyses, at C er stump så kunne vi finde den spidse vinkel C₁ ved at bruge sinusrelationerne (som vist ovenfor). Men da C₂ er den stumpe vinkel, kunne vi finde den ved hjælp af formlen ovenfor.

$$C_2=180^\circ-C_1=180^\circ-48,5^\circ=131,5^\circ$$

Grunden til at sammenhængen er sådan skyldes at

$$\sin(v)=\sin(180^\circ-v)$$

Dette kan illustreres ved følgende tegning

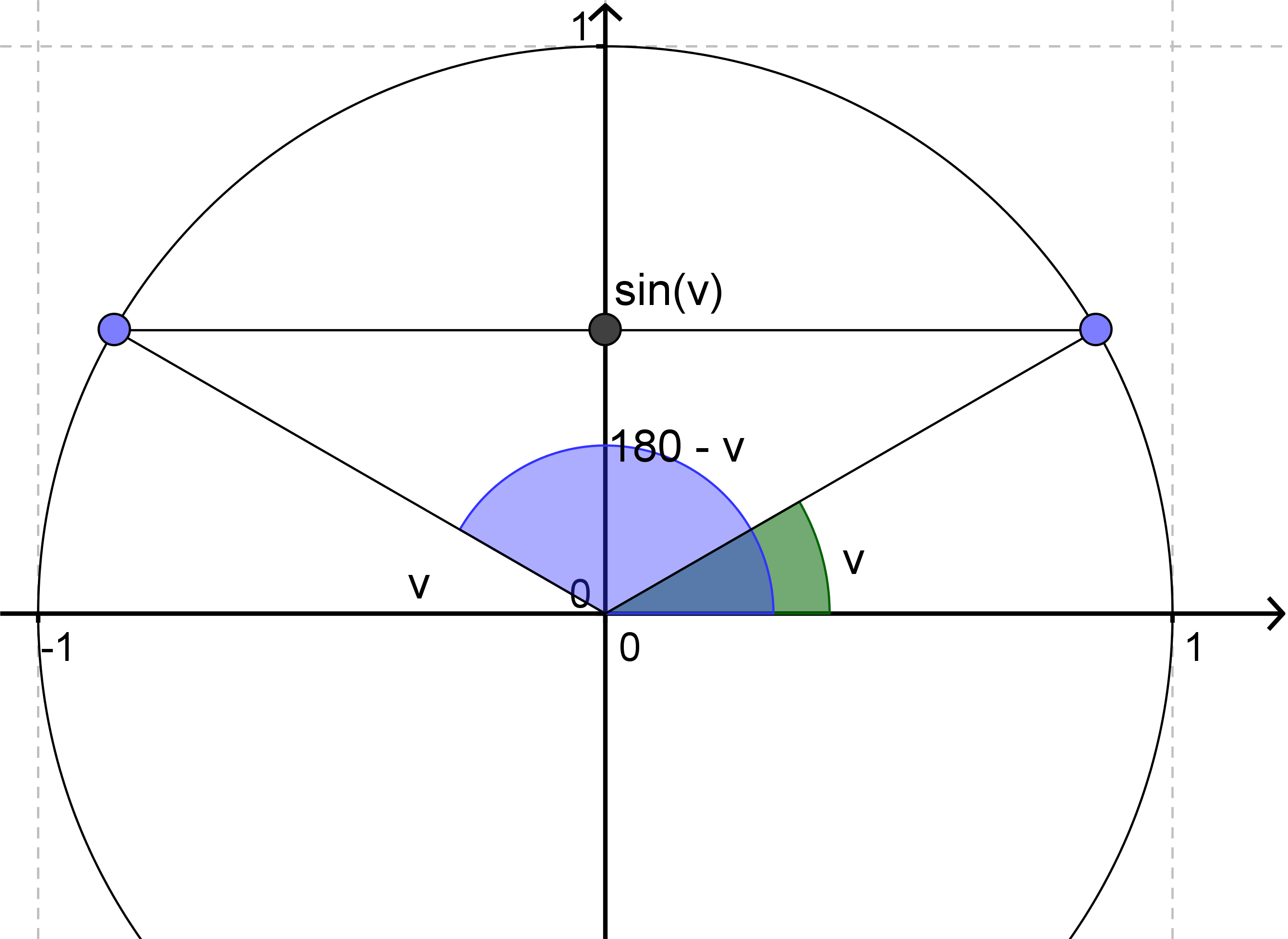
På illustrationen har vi indtegnet enhedscirklen og i denne har vi indtegnet en vinkel v (grøn) samt en vinkel, hvis størrelse er 180º-v (blå). Vi husker, at sinus til en vinkel findes ved at gå vandret ind fra skæringspunktet mellem vinkelbenet og enhedscirklen til man støder på y-aksen. Vi kan se, at de to vinkler har samme sinusværdi.

For at vende tilbage til vores eksempel, så startede vi jo med at regne ud, at sinC=0,75. Hvis vi markerer 0,75 på y-aksen i et koordinatsystem med enhedscirklen indtegnet, så kan vi ud fra denne sinusværdi konstruere to vinkler ved at gå vandret hhv til højre og venstre fra vores punkt.

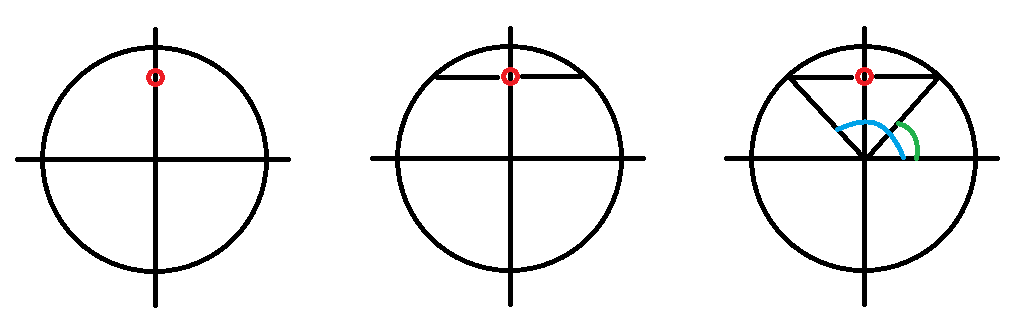
De to vinkler er hhv 48,5 og 131,5 grader store. Når man bruger sin^-1 på sin lommeregner, vil den altid give den spidse vinkel. Ønsker man i stedet den stumpe, skal man trække den spidse fra 180.

Videolektion