Grafisk lösning av ekvationer

Att lösa ekvationer sker antingen genom algebraisk ekvationslösning, eller grafiskt. I det här avsnittet introduceras metoden för grafisk lösning av ekvationer.

Vi löser en ekvation grafiskt genom att göra om båda leden till varsin funktion, som sedan ritas upp i samma koordinatsystem. \(x\)-värdet under skärningspunkten för de två funktionerna blir lösningen på ekvationen, eftersom det är där som ekvationens båda sidor är lika stora (VL=HL).

Exempel

Vi vill lösa följande ekvationen \(5x=87\) grafiskt. Efter uppdelning av båda leden till separata funktioner får vi:

$$\left\{\begin{matrix} y_{1}=5x \\ y_{2}=87 \end{matrix}\right.$$

Uppritat i ett koordinatsystem blir det som följande graf:

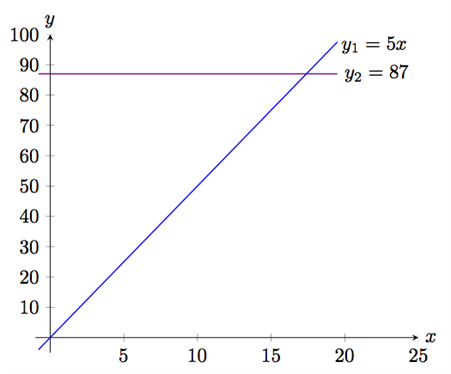
Skärningspunkten mellan de båda kurvorna har koordinaterna \((17,4;\; 87)\), vilket ger \(x=17,4\) som lösning på ekvationen.

Exempel

Om vi har ekvationen

$$x^3=87$$

som vi ska lösa grafiskt, då får vi på samma sätt som i det förra exemplet två funktioner:

$$\left\{\begin{matrix} y_{1}=x^{3} \\ y_{2}=87 \end{matrix}\right.$$

Uppritade i ett gemensamt koordinatsystem blir det så här:

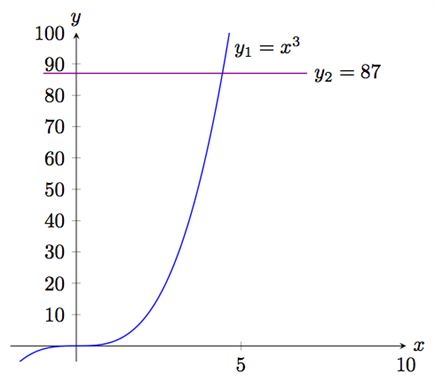
Skärningspunkten har de ungefärliga koordinaterna \((4,43;\; 87)\), vilket ger lösningen \(x≈4,43\).