Grafisk lösning av olikheter

I avsnittet olikheter lärde vi oss att lösa olikheter algebraiskt. I detta avsnitt bygger vi vidare på våra kunskaper genom att lära oss att olikheter kan även lösas grafiskt, på ett liknande sätt som ekvationer kan lösas grafiskt.

Exempel

Olikheten som ska lösas grafiskt är

$$197 + x ≤ 400$$

där vi är intresserade av vilka tal som \(x\) uppfyller olikheten. Vi börjar med att skriva olikheten som två funktioner, en funktion för vardera led:

$$\left\{\begin{matrix} y_{1}=&197+x\\ y_{2}=&400 \end{matrix}\right.$$

Dessa funktioner ritas upp i ett koordinatsystem enligt nedan. Har man inte tillgång till digitala hjälpmedel kan man rita för hand.

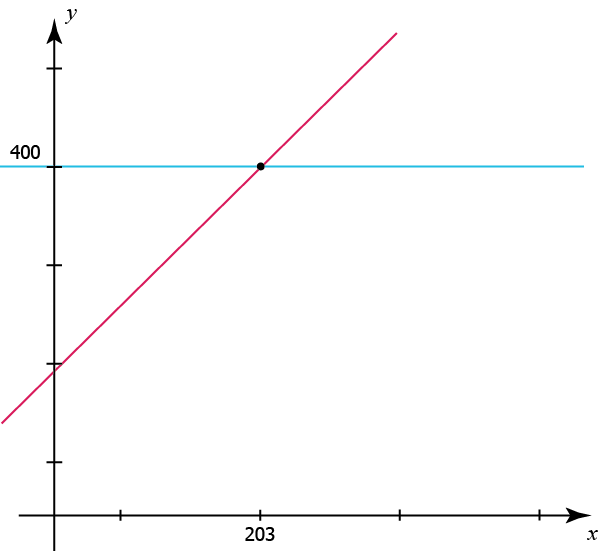
I grafen ser vi att skärningspunkten för de två linjerna är när \(x\) är \(203\). Men till skillnad från när vi löser en vanlig ekvation, så är alla \(x\)-värden från skärningspunkten möjliga lösningar till olikheten.

Lösningen på olikheten kommer alltså inte att utgöras av ett värde på \(x\), utan ett intervall av värden på \(x\).

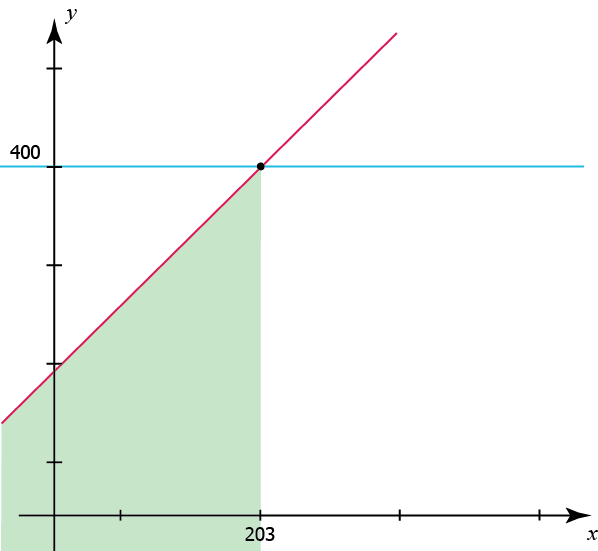
I figuren ovan ser vi att den grafiska lösningen av olikheten ger svaret att \(x\) ska ha ett värde som är mindre än eller lika med ungefär \(203\).