Räkna med vektorer

I det här avsnittet ska vi undersöka några räkneregler som gäller då vi använder oss av vektorer. Vi tittar på de generella samband som gäller och avslutar med en sammanfattning av räkneregler för vektorer.

Produkten av en skalär och en vektor

Som vi kortfattat kom in på i det förra avsnittet, är en skalär en storhet som kan beskrivas med hjälp av bara ett enda tal, till skillnad från vektorer som beskrivs av dess storlek och dess riktning tillsammans. Med andra ord är en skalär i detta sammanhang bara ett tal – en koefficient.

Om vi multiplicerar en vektor med en positiv skalär, då behåller vektorn sin tidigare riktning, men den får en ny storlek. Multiplicerar vi till exempel vektorn \(\overrightarrow{v}\) med skalären \(3\), så kommer vektorpilen att bli tre gånger längre dvs vektorns storlek ökar med en faktor \(3\), vilket vi visar i figuren nedan.

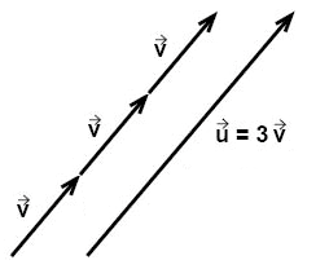
Vi kan använda ett exempel med en kraft för att förklara detta. En kraft har både en storlek och en riktning i vilken kraften verkar. Om vi tredubblar en kraft, så kommer vektorn att bli tre gånger så stor, men den kommer att behålla samma riktning som tidigare.

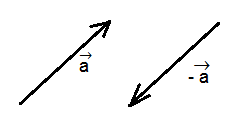
Om vi multiplicerar en vektor med en negativ skalär, då kommer den nya vektorn att få motsatt riktning och en ny storlek. Multiplicerar vi till exempel vektorn ovan med \(-3\), så kommer vektorn att bli tre gånger längre, men i det här fallet får den också motsatt riktning mot tidigare, vilket vi illustrerar i figuren nedan.

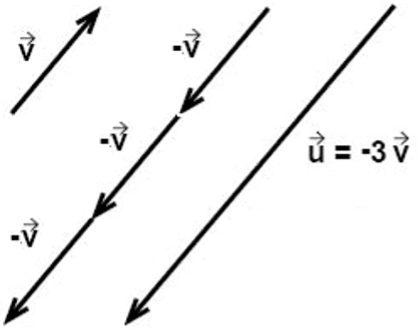
Addition av vektorer

När vi adderar två vektorer med olika riktningar kommer den nya vektorn få en annan storlek och riktning. Adderar vi två vektorer med samma riktning kommer storleken att ändras, men inte riktningen. Termerna i en vektoraddition kallas för komposanter och summan av komposanterna kallas resultant. I en figur kan man se summan av två vektorer som diagonalen i det parallellogram som bildas av de två vektorerna. Resultanten har markerats med en blå pil i figuren nedan):

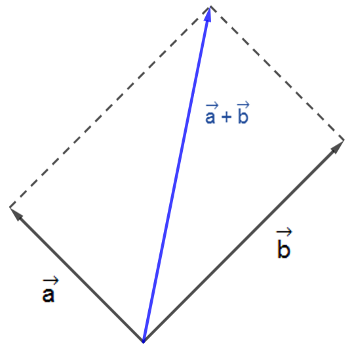
Man kan se det som att man parallellförflyttar den ena vektorn, vektorn \(\overrightarrow{b}\) i figuren nedan, så att dess startpunkt sammanfaller med den andra vektorns slutpunkt, vektorn \(\overrightarrow{a}\) i samma figur.

Då kommer summan av de två vektorerna att utgöras av den vektor som kan dras mellan den ena vektorns startpunkt och den parallellförflyttade vektorns slutpunkt.

Jämför med figuren ovan.

Subtraktion av vektorer

I avsnittet om negativa tal kom vi fram till att vi kan se subtraktion som samma sak som addition av ett negativt tal. På samma sätt kan man se subtraktion av en vektor som addition av motsvarande motsatta vektor (det vill säga den vektor som har motsatt riktning men samma storlek). Man kan skriva det så här:

$$ \overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})$$

Det här får vi göra eftersom om vi multiplicerar en vektor med skalären \((-1)\), så kommer vi att få en vektor med exakt samma storlek men med motsatt riktning, vad vi kallar en motsatt vektor.

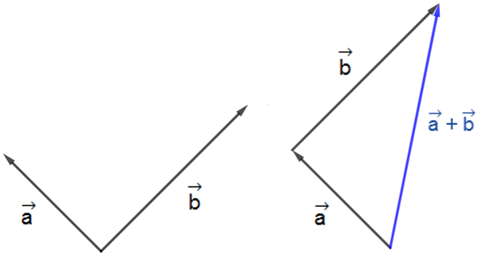
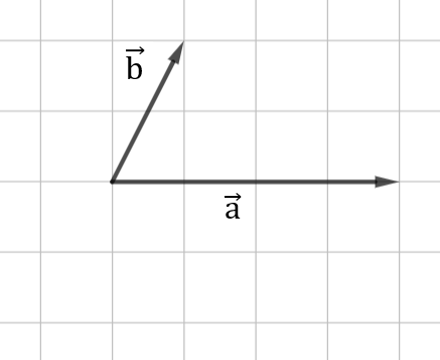
Om vi har två exempelvektorer \(\overrightarrow{a}\) och \(\overrightarrow{b}\) enligt figuren nedan

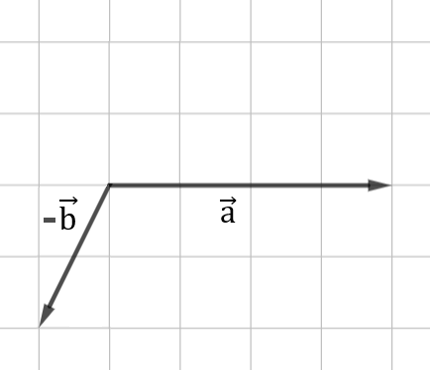
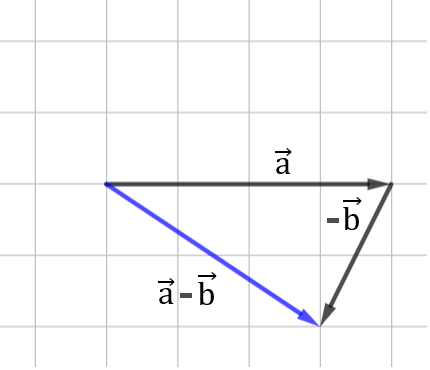
och ska komma fram till differensen mellan vektor \(\overrightarrow{a}\) och vektor \(\overrightarrow{b}\), då kan vi börja med att tolka om situationen som att vi istället vill ha summan av vektorn \(\overrightarrow{a}\) och vektorn \(-\overrightarrow{b}\):

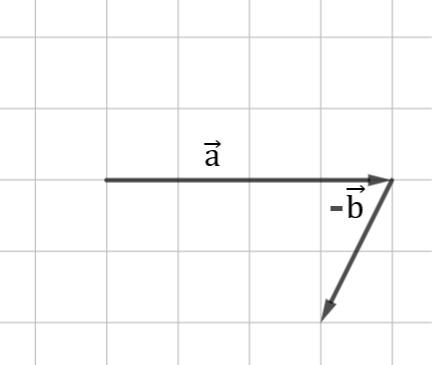
Därefter gör vi precis som vi kom fram till tidigare, när vi gick igenom addition av vektorer: vi parallellförflyttar en av vektorerna så att den ena vektorns startpunkt är densamma som den andra vektorns slutpunkt. Vi får då en figur enligt följande:

Den vektor \(\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}\) som bildas mellan vektor \(\overrightarrow{a}\):s startpunkt och vektor \((-\overrightarrow{b})\):s slutpunkt, är summan av vektorerna (resultanten).

Vektorer i koordinatform

Vi beskrev i det inledande avsnittet om vektorer att en vektor som har längden \(1\) kallas för en enhetsvektor. Vi kom också fram till att vi kan välja enhetsvektorer sådana att de har samma riktning som axlarna i ett koordinatsystem.

När vi väl har definierat sådana speciella enhetsvektorer, kan vi använda dem för att uttrycka andra vektorer.

Om vi ser vektorn \(\overrightarrow{a}\) som resultanten till två komposanter \(\overrightarrow{a}=\overrightarrow{a_x}+\overrightarrow{a_y}\) som är parallella med x-axeln respektive y-axeln, så kan vi uttrycka resultantens koordinater med hjälp av enhetsvektorer:

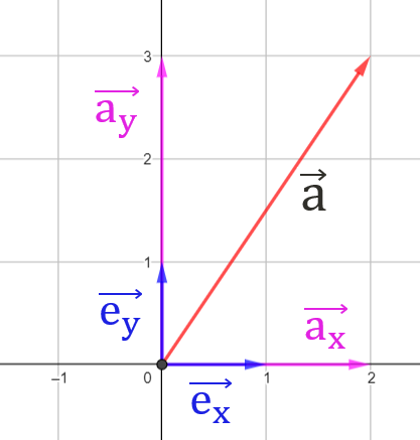
Komposanten \(\overrightarrow{a_x}\) kan skrivas som en skalär av enhetsvektorn \(\overrightarrow{e_x}\), medan komposanten \(\overrightarrow{a_y}\) kan skrivas som en skalär av enhetsvektorn \(\overrightarrow{e_y}\), enligt följande:

$$ \\\overrightarrow{a}=\color{Purple}{ \overrightarrow{a_x}+\overrightarrow{a_y} }=2\color{Blue}{ \overrightarrow{e_x} }+3\color{Blue}{ \overrightarrow{e_y} }=2\cdot\color{Blue}{(1,\;0)}+3\cdot\color{Blue}{(0,\;1)}=(2,\;3)$$

De koordinater \((2,\;3)\) som vi använder för att beskriva vektorn i koordinatform, är, som vi såg ovan, lika med skalärerna som vi multiplicerade respektive enhetsvektor med för att få vektorns komposanter.

Vill man addera två vektorer i koordinatform, kan man alltså addera de två vektorernas respektive komposanter, och därigenom få resultanten så här:

$$\\ \begin{align} \overrightarrow{a}+\overrightarrow{b} &=(a_x,\, a_y)\,+\,(b_x,\, b_y)= \\ &=(a_x + b_x,\, a_y + b_y) \end{align}$$

Med andra ord, addera helt enkelt x- och y-koordinaterna med varandra. Subtraktion fungerar på ett liknande sätt:

$$\\ \begin{align} \overrightarrow{a}-\overrightarrow{b} &=(a_x,\, a_y)\,-\,(b_x,\, b_y)= \\ &=(a_x - b_x,\, a_y - b_y) \end{align}$$

Slutligen, om vi multiplicerar en vektor med skalären \(s\) så kommer varje koordinat förstoras eller förminskas med faktorn \(s\):

$$s \overrightarrow{a}=s(a_x,\, a_y)=(sa_x,\, sa_y)$$

Exempel

Vi har de två vektorerna

$$\overrightarrow{a}=(2,\;3)$$

$$\overrightarrow{b}=(3,\;1)$$

och vi vill ta reda på vad \(\overrightarrow{a}+\overrightarrow{b}\) har för koordinater. Det görs genom att summera koordinaterna:

$$\overrightarrow{a}+\overrightarrow{b}=(2,\;3)+(3,\;1)=(2+3,\;3+1)=(5,\;4)$$

Om vi vill veta vad \(3\overrightarrow{a}\) är så skalar vi upp varje koordinat genom att multiplicera med \(3\):

$$3\overrightarrow{a}=3\cdot(2,\,3)=(3\cdot2,\,3\cdot3)=(6,\;9)$$

Sammanfattning av räkneregler för vektorer

Nu kan vi sammanfatta de räknereglerna för vektorer, skrivna i koordinatform, enligt följande generella samband:

• Addition av vektorer

$$\begin{align} \overrightarrow{a}+\overrightarrow{b} &=(a_x,\, a_y)\,+\,(b_x,\, b_y)= \\ &=(a_x + b_x,\, a_y + b_y) \end{align}$$

• Subtraktion av vektorer

$$\begin{align} \overrightarrow{a}-\overrightarrow{b} &=(a_x,\, a_y)\,-\,(b_x,\, b_y)= \\ &=(a_x - b_x,\, a_y - b_y) \end{align} $$

• Multiplikation med skalär

$$s \overrightarrow{a}=s(a_x,\, a_y)=(sa_x,\, sa_y)$$

där \(s\) är en skalär.