Rätblock, prisma och cylinder
I detta avsnittet lär vi oss hur vi beräknar volymen för några vanliga tredimensionella kroppar: rätblock, prismor och cylindrar. Vi bestämmer också hur de olika enheterna omvandlas.
Rätblock
Ett rätblock är en tredimensionell figur med enbart räta vinklar i dess åtta hörn, som ser ut som i illustrationen nedan. Man kan tänka på rätblock som figurer som har samma form som en typisk skokartong eller en tegelsten.
Ett annat sätt att tänka på rätblock är att man har en tvådimensionell figur i form av en rektangulär bottenyta. Sedan lägger man till ytterligare en dimension, genom att den rektangulära bottenytan lyfts uppåt och får en höjd till ett tredimensionellt rätblock.
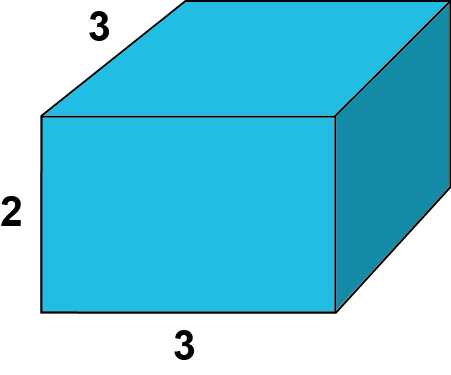
I figuren ovan har den rektangulära bottenytan en area som bestäms av de båda sidorna med längden \(3\) - rätblocket bildas genom att vi även tar med höjden i figuren, som har längden \(2\).
Om vi multiplicerar rätblockets bottenarea med dess höjd får vi rätblockets volym (V).
$${V}_{\text{rätblock}}=basen\cdot bredden\cdot höjden=basarean\cdot höjden$$
Volym mäts i kubikenheter. När rätblockets sidor har enheten meter blir volymen kubikmeter \((m^3)\). En kubikmeter motsvarar volymen på en kub som har sidan en meter, alltså \(1\,m\cdot1\,m\cdot1\,m=1\,m^3\). En kub är ett specialfall av rätblock, där alla rätblockets sidor har samma längd.
Om längdenheten i figuren ovan är meter, då får vi följande volym:
$$V=3\cdot 3\cdot 2=18m^3$$
Precis som med enheter för area kan vi visa hur vi omvandlar mellan enheter när det rör sig om volym:
$$1\,m^{3}=1(10\,dm)^{3}=10\,dm\cdot10\,dm\cdot10\,dm =10^{3}\;dm^{3}=1000\;dm^{3}$$
$$1\,dm^{3}=1(10\,cm)^{3}=10\,cm\cdot10\,cm\cdot10\,cm =10^{3}\;cm^{3}=1000\;cm^{3}$$
$$1\,cm^{3}=1(10\,mm)^{3}=10\,mm\cdot10\,mm\cdot10\,mm =10^{3}\;mm^{3}=1000\;mm^{3}$$
Omvandling:
$$m^3 \rightarrow dm^3\; \text{multipliceras med}\;10^3$$
$$dm^3 \rightarrow cm^3\; \text{multipliceras med}\;10^3$$
$$cm^2 \rightarrow mm^3\; \text{multipliceras med}\;10^3$$
Prisma
Ett prisma är en tredimensionell kropp, vars bottenyta har formen av en månghörning (till exempel en femhörning) och som har en viss höjd. Ett rätblock är ett specialfall av prisma, där bottenytan har formen av en rektangel; ett prisma kan dock ha många olika former på bottenytan, till exempel kan bottenytan vara triangulär.
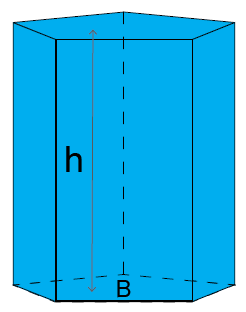
Volym för ett prisma motsvaras av bottenytans area B multiplicerad med prismats höjd h:
$$V_{\text{prisma}}=B\cdot h$$
Cylinder
En cylinder är liksom rätblocket en tredimensionell kropp, men för cylindrar gäller att deras bottenyta är cirkulär. Om den cirkulära bottenytan lyfts uppåt bildas en tredimensionell kropp i form av en cylinder.
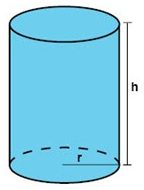
Volymen för en cylinder motsvaras av bottencirkelns area B multiplicerad med cylinderns höjd:
$$V_{cylinder}=B\cdot h=\pi \cdot r^{2}\cdot h$$
Begränsningsyta och mantelarea
Om vi summerar alla areor på alla ytor på en kropp, får vi den så kallade begränsningsytan. Den välvda ytan på en tredimensionell kropp (t ex cylinder eller kon) kallas för mantelyta. Man kan se dessa ytor som det "skal" som avgränsar de olika kropparna.
Mantelarea, med ett annat ord, är ytan runt sidan av en geometrisk form, exklusive toppen och botten, särskilt för en cylinder eller en prisma.
Till exempel beräknas mantelarean för cylindern genom att multiplicera höjden med omkretsen av dess bas.
$$\text{Mantelarea}_{cylinder}=\text{Höjd}\; x\; \text{basen}$$
Här går vi igenom hur vi beräknar volymen och arean av tredimensionella figurer.
Hjälpmedel
Här används grafräknaren Casio FX-CG20.
Se samma uppgift med grafräknaren Casio FX-9750GII.
Grafräknare av andra fabrikat har ungefär motsvarande funktionalitet.
- Tvådimensionell: Något som befinner sig i ett plan. Något som har två riktningar (dimensioner), t ex en area.
- Tredimensionell: Något som befinner sig i rummets samtliga tre dimensioner. T ex en kub, eller en cylinder.
- Enhet: En enhet är ett ord eller ett namn som betecknar något. Vi använder enheter när vi vill tillexempel berätta om hur mycket något är eller hur många saker är.
- Kvadratenheter: Måttenhet för area.
- Kubikenheter: Måttenhet för volym.
- Mantelarea: Är ytan runt sidan av en geometrisk form, exklusive toppen och botten.
