Vektorer

I detta avsnitt ska vi introducera ett nytt begrepp: vektorer. En vektor är ett föremål som har både en storlek (magnitud) och riktning. Exempelvis kan en hastighet vara en storhet som har en riktning (vänster, höger, framåt, bakåt, etc.) och en storlek (man kan köra olika fort).

Vektorer

En vektor är en storhet som har både en storlek (magnitud) och en riktning, till skillnad från en skalär, som är en storhet som enbart har en storlek (till exempel en volym eller en temperatur).

Andra exempel på storheter som kan beskrivas som vektorer är kraft och acceleration. Användning av vektorer, med de räkneregler som gäller för dessa, kan underlätta när vi till exempel har en situation där olika stora krafter verkar i olika riktningar på ett föremål och vi är intresserade av vilken påverkan dessa krafter har sammantaget.

Vektorer betecknas oftast med bokstäver med en pil ovanför, för att tydliggöra att det är en storhet med såväl storlek som riktning. Här är ett exempel på hur man kan visa detta:

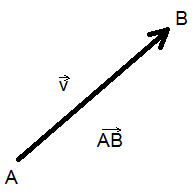
där vektorn \(\overrightarrow{v}=\overrightarrow{AB}\)

Ett annat vanligt sätt är att använda fetstil för att markera att storheten är en vektor. Alltså hade vektorn i fråga skrivits som v.

Ett sätt att åskådliggöra en vektor i en figur är att från en startpunkt (A) rita en pil i riktning mot slutpunkten (B).

Vektorer som har samma längd och samma riktning är likadana (pilens längd representerar vektorns storlek/magnitud, medan vart pilen pekar visar vektorns riktning).

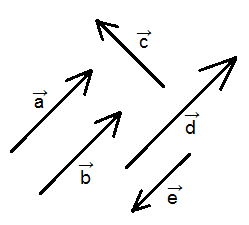
I bilden ovan är vektorerna \(\overrightarrow{a} \, och \, \overrightarrow{b} \) lika. De är visserligen förskjutna relativt varandra, men när man avgör om två vektorer är lika behöver man bara ta i åtanke deras storlek och riktning.

Parallella vektorer

Två vektorer är parallella om de har samma eller motsatt riktning. Att två vektorer (eller linjer i ren allmänhet) är parallella kan markeras med hjälp av två parallella streck: ||

I figuren ovan gäller det att \(\overrightarrow{a} \text{||} \overrightarrow{b}\). Det gäller också att \(\overrightarrow{a}\) är parallell med \(\overrightarrow{d}\) och \(\overrightarrow{e}\). Vektorerna \(\overrightarrow{a}, \overrightarrow{b}\) och \(\overrightarrow{d}\) har samma riktning medan \(\overrightarrow{e}\) har motsatt riktning.

Vektorers storlek

Längden på en vektor kallas även för vektorns storlek eller vektorns absolutbelopp, och betecknas

$$\left | \overrightarrow{v} \right | $$

Längden på en vektor får man genom att använda Pythagoras sats.

Låt oss titta på ett exempel där vi beräknar en vektors längd:

Vi vill räkna ut längden på vektorn \(\overrightarrow{v}\) som avbildats i koordinatsystemet nedan:

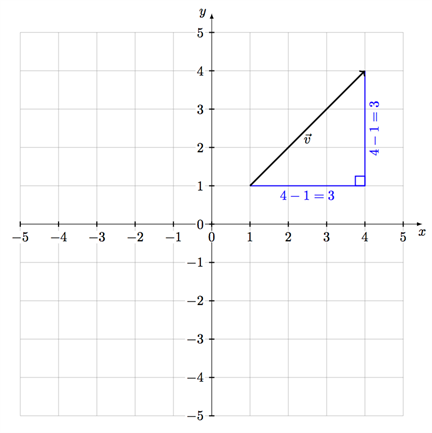
För att göra detta tar vi först reda på längden på katetrarna i den rätvinkliga triangel som bildas om vi delar upp vektorns längd längs x-axeln och y-axeln.

Längden på de båda katetrarna blir \(4-1=3\) längdenheter, vilket vi nu använder i Pythagoras sats för att få ut längden på hypotenusan (som ju motsvarar längden på vektorn):

$$\left | \vec{v} \right |\;=\;\sqrt{\left ( 4\;-1 \right )^{2}+\left ( 4\;-\;1 \right )^{2}}=\sqrt{3^{2}\;+\;3^{2}}=\sqrt{18}\approx 4,24$$

För en vektor \(\overrightarrow{AB}\) från punkten \(A=(x_1,\,y_1)\) till \(B=(x_2,\,y_2\) gäller det alltså att:

$$|\overrightarrow{AB}|=\sqrt{(∆x)^2+(∆y)^2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$

Om vektorn \(\overrightarrow{v}=(x,y)\) utgår från origo gäller det specifikt att:

$$|\overrightarrow{v}|=\sqrt{(∆x)^2+(∆y)^2}=\sqrt{(x-0)^2+(y-0)^2}$$

$$|\overrightarrow{v}|=\sqrt{(x)^2+(y)^2}$$

Parallellförflyttning av vektorer

En vektor kan flyttas i ett koordinatsystem parallellt med sin riktning utan att längden eller riktningen på vektorn ändras. Det kallas att man parallellflyttar vektorn och kan användas för att flytta vektorn till origo.

Fördelen med att ha en vektor som har sin startpunkt i origo är att man kan representera vektorn med slutpunktens koordinater. En sådan representation innebär att vi entydigt anger såväl vektorns storlek som dess riktning med hjälp av endast de två koordinaterna.

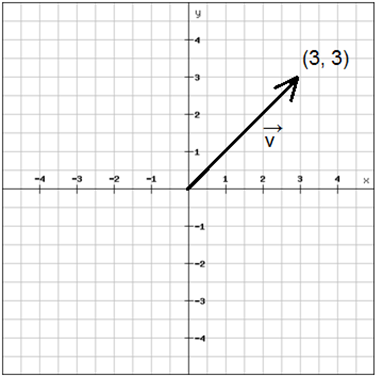
Vår vektor från exemplet ovan kan vi därför entydigt beskriva som

$$\overrightarrow{v}=\left ( 3,\;3 \right )$$

Vi säger att vektorn är skriven i koordinatform.

Enhetsvektorer

En vektor som har längden \(1\) kallas för en enhetsvektor. Enhetsvektorer används oftast när man är mer intresserad av att beskriva enbart riktningen på någon kraft eller annan fysisk storhet.

Det är inte helt ovanligt att enhetsvektorer skrivs på ett speciellt sätt:

$$\Large{\hat v}$$

Man sätter en liten ”hatt” på vektorn för att markera att dess absolutbelopp är \(1\). Detta utläses även som ”v-hatt”.