Lotto

Spelet Lotto går ut på att man ska välja 7 nummer av totalt 35 stycken. Dragningen går sedan till så att 7 stycken bollar plockas slumpmässigt (maskinellt) utan återläggning.

Beräkna sannolikheten att få exakt 7, 6 respektive 5 rätt på Lotto.

Svara på formen: "Sannolikheten är 1 på x att få y rätt, ...".

n! = 1∙2∙...∙(n-1)∙n (uttalas "n-fakultet") kan vara smidigt att använda vid beräkningen för att få en kompakt notation.

Lösningsförslag:

7 rätt

Vi kan beräkna sannolikheten stegvis genom att gå igenom nummer för nummer:

P(7 rätt) = P(mitt 1:a nummer finns bland de 7 vinstnumren) ∙ P(mitt 2:a nummer finns bland de återstående 6 vinstnumren) ∙ ... ∙ P(mitt 7:e nummer är lika med det sista återstående vinstnumret) =

$$\\\frac{7}{35}\cdot \frac{6}{34}\cdot \frac{5}{33}\cdot \frac{4}{32}\cdot \frac{3}{31}\cdot \frac{2}{30}\cdot \frac{1}{29}=\\\\=\frac{7!}{\frac{35!}{28!}}=\frac{7!\cdot 28!}{35!}=1,4871\cdot 10^{-7}$$

Det innebär att sannolikheten att få 7 rätt är 1 på 1/(1,4871∙10^-7), d.v.s. 1 på 6,7 ∙ 10⁶ =

6,7 miljoner.

6 rätt

För att räkna ut sannolikheten att få exakt 6 rätt får vi först tänka ut på hur många olika sätt man kan få 6 rätt. Antingen kan första, andra, o.s.v. numret vara fel. Något av de sju numren är alltså fel. Därför fås sambandet: P(exakt 6 rätt) = 7 ∙ P(mitt 1:a nummer är fel och resten rätt).

P(exakt 6 rätt) = 7 ∙ P(1:a numret fel) ∙ P(2:a numret rätt) ∙ P(3:e numret rätt) ∙ ... ∙ P(7:e numret rätt) =

$$\\7\cdot \frac{28}{35}\cdot \frac{7}{34}\cdot \frac{6}{33}\cdot \frac{5}{32}\cdot \frac{4}{31}\cdot \frac{3}{30}\cdot \frac{2}{29}=\\\\=\frac{7 \cdot 28\cdot 7!}{\frac{35!}{28!}}=\frac{7 \cdot 28\cdot 7!\cdot 28!}{35!}=2,9147\cdot 10^{-5}$$

Det innebär att sannolikheten att få exakt 6 rätt är 1 på 1/(2,9147∙10^-5), d.v.s. 1 på 34309.

5 rätt

För att räkna ut sannolikheten att få exakt 5 rätt får vi först tänka ut på hur många olika sätt man kan få 5 rätt. Antingen kan första och andra numret vara fel, första och tredje o.s.v. Vi får nedanstående tabell av kombinationer:

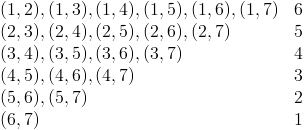
Sammanlagt har vi alltså: 6+5+4+3+2+1 = 21 olika kombinationer som alla är lika sannolika.

$$\\1+2+...+(n-1)+n=\frac{n(n+1)}{2}\\\\1+2...+5+6=\frac{6\cdot (6+1)}{2}=\frac{42}{2}=21$$

är ett alternativt sätt att räkna ut summan som kan vara användbart när n är stort.

P(exakt 5 rätt) = 21 ∙ P(1:a numret fel) ∙ P(2:a numret fel) ∙ P(3:e numret rätt) ∙ ... ∙ ∙ P(7:e numret rätt)=

$$\\21\cdot \frac{28}{35}\cdot \frac{27}{34}\cdot \frac{7}{33}\cdot \frac{6}{32}\cdot \frac{5}{31}\cdot \frac{4}{30}\cdot \frac{3}{29}=\\\\=\frac{21\cdot 28\cdot 27\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3}{\frac{35!}{28!}}=\\\\=\frac{21\cdot 28\cdot 27\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 28!}{35!}=1,1805\cdot 10^{-3} $$

Det innebär att sannolikheten att få exakt 5 rätt är 1 på 1/(1,1805∙10^-3), d.v.s. 1 på 847.

Sannolikheten att få 7 rätt är 1 på 6,7 miljoner, exakt 6 rätt 1 på 34309 och exakt 5 rätt 1 på 847.