Talbaser

Tidigare har vi utgått från att det är självklart hur ett tal, till exempel 42, ska tolkas. Men om vi ser på saken ur ett större perspektiv visar det sig att det idag finns, och historiskt har funnits, flera olika talsystem, som bestämmer hur vi anger tals värden utifrån något som kallas positionssystemet. I det här avsnittet ska vi gå igenom positionssystemet och några av de vanligare förekommande talsystem och olika talbaser.

Positionssystemet

Talsystem som vi är vana vid följer positionssystemet. I ett positionssytemet är det siffrornas position i talet som avgör värdet på siffran. Alla siffror har alltså olika värden beroende på var i talet de befinner sig. Siffran längst till vänster har högst värde och siffran längst till höger har lägst värde.

Talsystemet vi använder oss av kallas det decimala talsystemet och är ett positionssytem.

Det decimala talsystemet

Det decimala talsystemet är det talsystem som vi använder oss av.  Detta talsystem är samma som talbas 10 och består av tio siffror: 0,1,2,3,4,5,6,7,8,9. Varje siffra i ett tal är värd olika mycket beroende på positionen av siffran. Om vi undersöker decimaltalet 528,149 är positionerna följande:

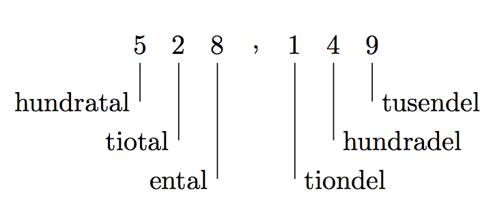
Som vi ser är siffran 5 värd 500 eftersom den är på positionen hundratal, siffran 2 är värd 20 eftersom den är på positionen tiotal, och så vidare. Det är alltså placeringen som avgör hur mycket en siffra är värd, vad den representerar.

Varje förflyttning av decimaltecknet åt höger eller vänster multiplicerar (höger) eller delar (vänster) siffrornas värde med 10. Flyttar vi decimaltecknet åt höger ändrar varje förflyttning det värde som siffran representerar med en faktor 10.

Om vi undersöker talet 42, vad betyder det egentligen? Enligt vårt talsystem betyder det fyra tiotal och två ental. Detta kan vi också skriva som en summa på förljande sätt:

$$42=40+2=4\cdot 10^{1}+2\cdot 10^{0}$$

Detta är ett ytterligare sätt att visa siffrornas värde i den position de har.

Det binära talsystemet

Det finns talsystem uppbyggda utifrån ett annat antal siffror än 10. Ett exempel är det binära talsystemet. "Bi" betyder två och det binära talsystemet heter som det gör därför att det endast använder två siffror: noll och ett. Alltså är det talbasen 2. Ett vanligt förekommande användningsområde för det binära talsystemet är inom digital elektronik, till exempel datorer. Det binära talsystemet är också ett positionssystem.

I den decimala världen ökar eller minskar värdet som representeras av en siffra med en faktor 10 beroende på siffrans placering i ett tal. I den binära världen ökar eller minskar värdet istället med en faktor 2.

Till exempel om vi har talet 10011, som består av två siffror (noll och ett). Dessa siffror ingår i både det decimala talsystemet och det binära talsystemet. Skriver vi talet enligt det decimala talsystemet, så menar vi:

$$10011=1\cdot 10^{4}+0\cdot 10^{3}+0\cdot 10^{2}+1\cdot 10^{1}+1\cdot 10^{0} $$

Vilket även kan skrivas som

$$\begin{align}10011 & =10000+0+0+10+1=\\ & =10000+10+1=\\ & =10000+11 \end{align}$$

och det sättet ger oss också talet 10011 skrivet i det decimala talsystemet.

Om vi har talet 10011 skrivet enligt det binära talsystemet, så menar vi enligt det decimala talsystemet följande:

$$\begin{align}10011 & =1\cdot 2^{4}+0\cdot 2^{3}+0\cdot 2^{2}+1\cdot 2^{1}+1\cdot 2^{0}=\\ & =16+0+0+2+1=19 \end{align}$$

Vilket innebär att talet 10011 i det binära talsystemet motsvarar 19 i det decimala talsystemet. 

Som vi vet kan varje tal skrivas i flera termer beroende på talets värde. Varje term består av en siffra som multipliceras med en bas upphöjt till en potens, vilket vi sett i tidigare exempel. Basen representerar antalet siffror i talsystemet. I det decimala talsystemet är basen 10 eftersom detta talsystem innehåller tio siffror (0,1,2,3,4,5,6,7,8,9). I det binära talsystemet är basen 2, eftersom det består av två siffror (0,1). Potensen representerar siffrans position i talet (eftersom för entalets position är potensen 0, tiotalets position är 1, hundratalets position är 2 osv). För att omvandla ett tal skrivet enligt det decimala talsystemet till det binära talsystemet, skriver vi talet som en summa av tvåpotenser, på samma sätt som vi gjorde ovan, där fick vi att 10011 i det binära talsystemet motsvarar 19 i det decimala talsystemet.

För att kunna skilja tal skrivna i olika baser från varandra brukar vi skriva ut talbasen i form av ett tal som står snett nedanför till höger om de övriga siffrorna i talet. Därigenom kan vi tydligt visa om vi menar ett tal skrivet i till exempel det decimala systemet.

$$10011_{10}$$

eller det binära systemet

$$10011_{2}$$

Talsystem med olika baser

Det finns flera olika talsystem som är uppbyggda med andra antal siffror än det binära talsystemet och det decimala talsystemet. Alla olika talsystem har en bas som anger hur många siffror vi får använda i just det talsystemet. Om vi tar talbasen 5, då får vi bara använda fem siffror (0, 1, 2, 3 och 4). Precis som med det decimala talsystemet (som har basen tio) och det binära talsystemet (som har basen två) så är det positionerna på ett tal som anger hur mycket en siffra är värd. Alla dessa talsystem med olika baser är också positionssytem.

Om vi har talet 343 skrivet i basen fem, kan vi skriva det som 343₅ för att förtydliga att vi menar just basen fem. Vill vi skriva om talet till bas tio gör vi följande:

$$343_5=(3\cdot 5^2+4\cdot 5^1+3\cdot 5^0)_{10}=(3\cdot 25+4\cdot 5+3\cdot 1)_{10}=98_{10}$$

Ett tal med basen fem menar då att positionerna är hur många av varje potens av 5 vi har. Därför får vi, från höger till vänster, ental, femtal, tjugofemtal, hundratjugofemtal, och så vidare.

Vi tittar på ett till exempel med talbasen 9

$$133_9= (1\cdot 9^2 + 3\cdot 9^1 +3 \cdot 9^0)_{10}= (81+27+3)_{10}= 111_{10}$$

Här hade vi från höger till vänster ental, niotal och åttioental och fick \(133_9= 111_{10}\).