Korrelation och regressionsanalys
I det här avsnittet ska vi titta närmare på de båda besläktade begreppen korrelation och regressionsanalys. Med hjälp av dessa begrepp kan vi finna samband i serier av observationsvärden, som vi i sin tur kan använda för att få en bättre förståelse för de fenomen som vi undersöker i olika sammanhang.
Korrelation
Vi bestämmer oss för att göra en undersökning där vi den första måndagen i varje månad under ett helt års tid räknar antalet personer på en tågperrong mellan klockan 9 och 10. När året är slut så sammanställer vi resultaten i en tabell enligt nedan.
| Månad | jan | feb | mar | apr | maj | jun | jul | aug | sep | okt | nov | dec |
| Antal människor | 20 | 100 | 105 | 97 | 205 | 158 | 79 | 122 | 180 | 116 | 99 | 86 |
I ett spridningsdiagram låter man den ena variabeln, kallad den förklarande variabeln, finnas längs x-axeln, och den andra variabeln, responsvariabeln, finnas längs y-axeln. I vårt exempel är vilken månad det är den förklarande variabeln och antalet räknade personer på perrongen responsvariabeln. För varje tillgängligt värde på den förklarande variabeln markerar vi in dess motsvarande värde för responsvariabeln (i vårt fall är till exempel ett av värdena på den förklarande variabeln "mars" och motsvarande värde på responsvariabeln 105 personer). Utifrån denna serie observationsvärden kan vi sedan undersöka om det finns något samband mellan vilken månad det är och antalet personer som befunnit sig på perrongen. Detta gör vi inledningsvis genom att rita in våra observationsvärden i ett spridningsdiagram.
Markerar vi på detta sätt varje par av värden på den förklarande variabeln och responsvariabeln i ett spridningsdiagram, så ser det i vårt exempel ut på följande sätt:
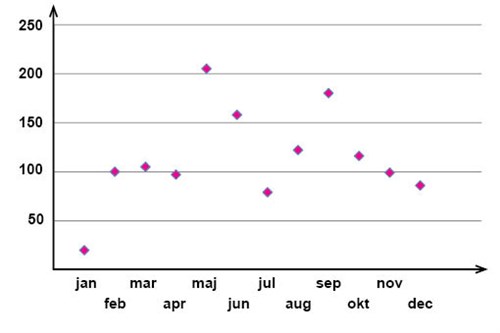
Utifrån ett spridningsdiagram kan man sedan få en uppfattning om huruvida det finns något samband, eller korrelation, mellan den förklarande variabeln och responsvariabeln.
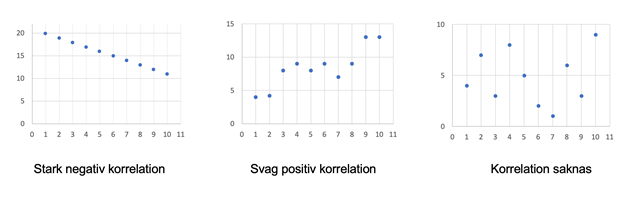
Om observationsvärdena som man har markerat i spridningsdiagrammet ligger samlade runt en tänkt linje med positiv lutning, så säger man att det finns en positiv korrelation mellan den förklarande variabeln och responsvariabeln. Detta är fallet för serien som markerats i diagrammet nedan.
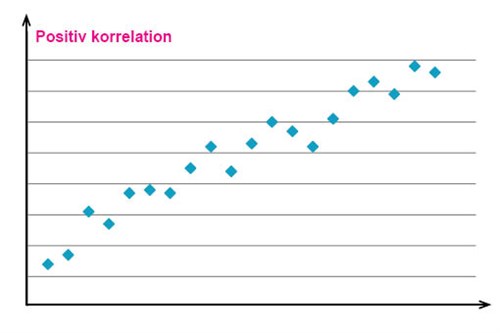
Om de observationsvärden som man markerat däremot ligger samlade runt en tänkt linje med en negativ lutning, så kallar man detta en negativ korrelation mellan den förklarande variabeln och responsvariabeln, vilket vi ser ett exempel på i diagramet nedan.
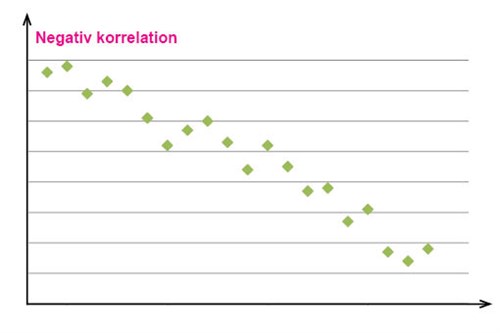
I ett fall som vårt exempel i början av avsnittet, där det varken verkar finnas en positiv eller negativ korrelation mellan variablerna, säger man att korrelation saknas och vi kan då dra slutsatsen att det utifrån våra observationsvärden inte tycks finnas något samband mellan vilken månad det är och hur många personer som befinner sig på perrongen.
Något som är viktigt att komma ihåg när vi gör korrelationsundersökningar, är att bara för att det finns en korrelation mellan de variabler vi tittar på, så behöver det inte finnas ett orsakssamband. Med detta menar vi att även om det finns en korrelation mellan variablerna, så kan det finnas någon annan variabel som inte finns med i vår analys, som förklarar varför våra variabler samvarierar.
Om vi till exempel gör en undersökning där vi jämför ålder med förekomst av en viss sjukdom, så kan det vara så att det finns en stark positiv korrelation mellan hur gammal en person är och hur vanligt förekommande sjukdomen är. Dock kan vi inte utan vidare dra slutsatsen att det är hög ålder som orsakat sjukdomen, då det kan finnas andra faktorer som spelar in, till exempel levnadsvanor, förekomst av andra sjukdomar, kostvanor tidigare i livet, etc. Därför bör man vara försiktig med att dra slutsatser om att man funnit ett orsakssamband, när man egentligen bara kan ha funnit en korrelation mellan de studerade variablerna.
Regressionsanalys
Vi kan utifrån ett spridningsdiagram där vi ser ett linjärt samband (antingen positiv eller negativ korrelation) beskriva sambandet med en linjär modell eller med andra ord beskriva sambandet med hjälp av räta linjens ekvation på formen
$$f(x) = kx + m$$
När vi söker efter en linjär modell som beskriver sambandet mellan våra variabler, kallar man detta linjär regression eller regressionsanalys. Vad vi söker är alltså en linje som våra markerade punkter avviker så lite från som möjligt. Har vi ett spridningsdiagram så kan vi för hand rita in en sådan ungefärlig linje och sedan ta reda på linjens k-värde och m-värde, på samma sätt som vi gjort tidigare utifrån kända punkter. Den räta linjens ekvation som vi försöker att komma fram till kallas den mest anpassade ekvationen och är den linje där avvikelsen från de markerade punkterna/mätvärdena i diagrammet är så liten som möjligt.
För att få fram en så exakt linjär anpassning som möjligt, använder man sig till exempel av sådana inbyggda funktioner för att göra linjär regression som finns på många grafritande miniräknare.
När man genom regressionsanalys väl har funnit en ekvation som så gott det går beskriver det statistiska underlag som man har, kan man sedan använda denna linjära modell till att förutse vad man kommer att få för värden vid andra mätpunkter.
Medellängden på svenska barn
I spridningsdiagrammet nedan har vi markerat in medellängden (responsvariabel; längs y-axeln) på svenska barn i åldrarna 1-16 år (den förklarande variabeln; längs x-axeln).
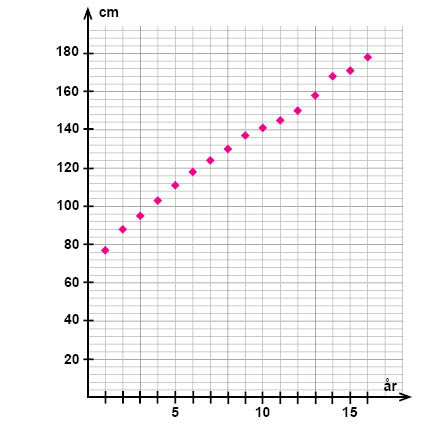
Som vi kan se så verkar det finnas en positiv linjär korrelation mellan åldern och den genomsnittliga längden. Därför kan vi försöka att hitta en linjär modell för sambandet med hjälp av en linjär regressionsanalys.
Vi börjar med att dra en rät linje som ligger på ett sådant sätt att avvikelsen mellan linjen och punkterna blir så liten som möjligt.
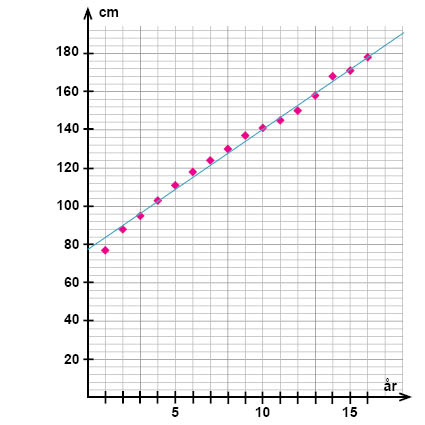
När vi nu har en rät linje markerad i vårt spridningsdiagram, kan vi, som för vilken annan rät linje som helst, läsa av koordinaterna för två godtyckliga punkter längs linjen. Dessa punkter behöver inte vara någon av de punkter som vi markerat i diagrammet; punkterna längs linjen som vi läser av får även gärna ligga en bra bit ifrån varandra längs linjen, så att eventuella avläsningsfel blir mindre betydelsefulla.
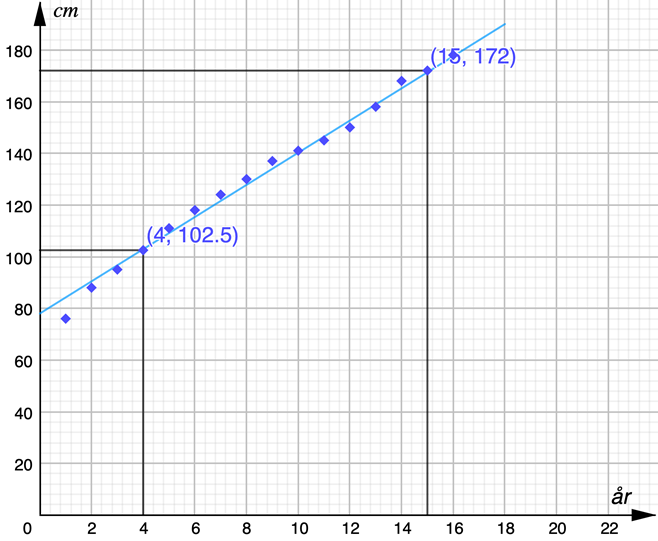
I spridningsdiagrammet ovan har vi markerat de båda punkterna (4; 102,5) och (15; 172).
När vi väl har funnit koordinaterna för två punkter längs linjen, använder vi dessa för att beräkna lutningen på vår linje:
$$k=\frac{172-102,5}{15-4}=\frac{69,5}{11}\approx6,3$$
I nästa steg beräknar vi räta linjens ekvation i dess helhet, med hjälp av antingen k-formen eller enpunktsformen.
Vi använder oss här av k-formen, sätter in de kända koordinaterna för en av punkterna längs linjen och får ut konstanttermen m:
$$f(x)=kx+m$$
$$172=\frac{69,5}{11}\cdot 15+m$$
$$m=172-\frac{69,5\cdot 15}{11}\approx77$$
När vi nu känner till värdet på såväl riktningskoefficienten k som konstanttermen m, har vi vår sökta räta linjes ekvation:
$$f(x)=6,3x+77$$
Detta är alltså det linjära samband som vi har funnit mellan ålder, x, och genomsnittlig längd, y, utifrån vårt statistiska material.
Som vi skrev tidigare så kan man använda en linjär regression för att förutse framtida värden, det vill säga i vårt exempel vilken längd barn i allmänhet kommer att ha vid olika åldrar. Vi kan utifrån det linjära sambandet förutse ungefär hur lång en 13-åring är:
$$f(13)=6,3\cdot 13+77=158,9\,cm$$
En linjär regression, om analysen har utförts rätt, stämmer väl i det intervall vi undersökt och ofta även en bit utanför detta, men ju längre bort från det intervall vi fått den linjära regressionen ifrån, desto sämre fungerar ofta modellen. Skulle vi använda vår linjära modell ovan för att ta reda på hur lång en 50-åring är, så får vi det till
$$f(50)=6,3\cdot 50+77=392\,cm$$
En 50-åring av normallängd skulle enligt den här modellen alltså vara ca 3,92 meter lång, vilket visar på att modellen inte är tillämpbar på vuxna människor (eftersom människor normalt slutar att växa på längden i 18-20årsåldern).
Det är även troligt att vår linjära modell är dålig på att förutse riktigt unga barns längd, till exempel då barnet är nyfött, det vill säga 0 år gammalt (vilket vi även kan ana oss till om vi tittar i spridningsdiagrammet för åldern 1 år). Enligt vår modell bör ett 0 år gammalt barn ha en längd på 77 cm, men i själva verket är genomsnittslängden för nyfödda barn ca 50 cm.
Vi avslutar med att visa i ett exempel hur vi kan låta GeoGebra skapa en linjär modell över sambandet åt oss.
Ett konditori sålde semlor under åtta veckor mellan januari och mars och förde statistik över hur priset på semlor påverkade försäljningen. Tabellen nedan visar resultatet.
| Priset per semla (kr) | Antal sålda semlor |
| 36 | 1009 |
| 64 | 440 |
| 72 | 383 |
| 45 | 660 |
| 54 | 635 |
| 42 | 732 |
| 39 | 875 |
| 60 | 618 |
Anpassa en rät linje till mätpunkterna, ange linjens ekvation och vilken sorts korrelation sambandet visar.
Lösning:
Vi börjar med att öppna GeoGebra, vi kommer denna gång använda Geogebra classic och öppna ett kalkylblad och föra in värdena i tabellen så här.
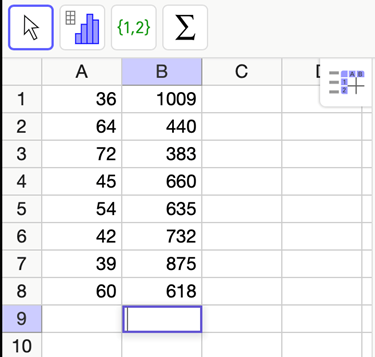
Sedan markerar vi alla våra värden och klickar på stapeldiagrammet längst upp och väljer Tvåvariabels regressionsanalys som vi kan se i bilden nedan.

Då får vi upp ett spridningsdiagram som ser ut som följande:
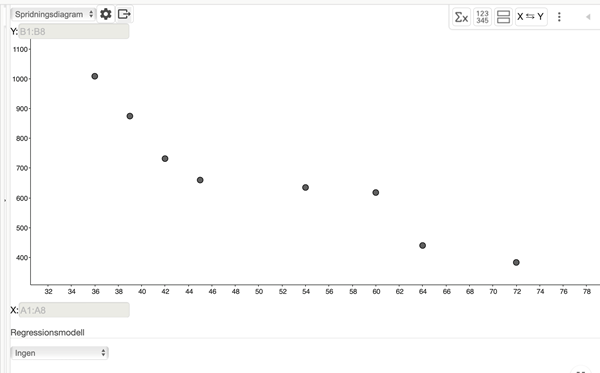
För att skapa vår linjära modell, så väljer vi Linjär i rullgardinsmenyn
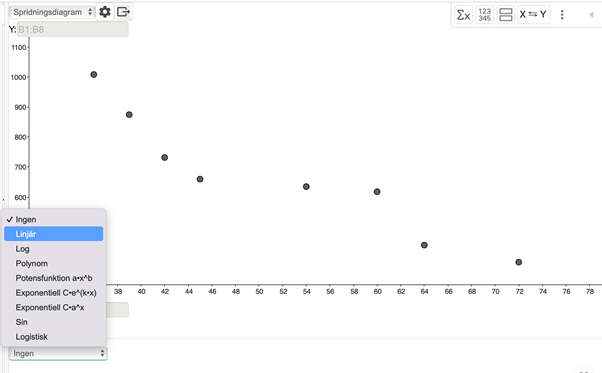
Då skapas vår linje i spridningsdiagrammet direkt och längs ner kan vi läsa av linjens ekvation.
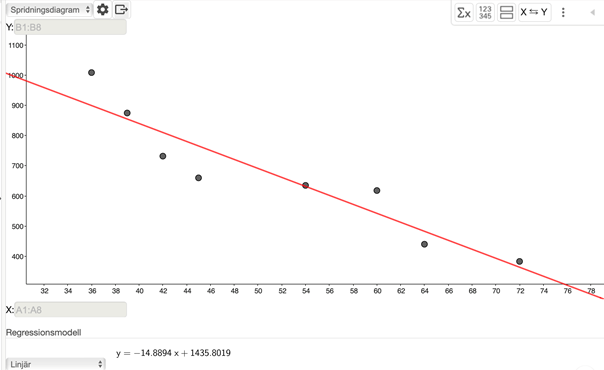
Så svaret blir alltså att linjens ekvation till vår linjära modell är ungefär (avrundat till heltal) \(f(x) = -15x + 1436\) och vi kan se att sambandet motsvarar en negativ korrelation.
Sammanfattning
Korrelation beskriver samband, både i styrka och riktning
Regressionsanalys är att vi försöker beskriva sambandet med en linjär modell med hjälp av räta linjens ekvation på formen \(f(x) = kx + m \)
Genomgång av korrelation.
Genomgång av regressionsanalys.
- Korrelation: visar ett samband mellan variabler, kan också beskriva riktning och styrka för sambandet.
- Förklarande variabel: den variabel som motsvarar x-axeln, oftast är det en variabel så som tid
- Responsvariabel: den variabel som motsvarar y-axeln
- Spridningsdiagram: en typ av diagram som visar observationer som punkter i ett koordinatsystem
- Positiv korrelation: betyder att om förklarande variabeln ökar så kommer även responsvariabeln öka, i ett spridningsdiagram är värdena samlade kring en linje med positiv lutning.
- Negativ korrelation: betyder att om förklarande variabeln ökar så kommer responsvariabeln minska, i ett spridningsdiagram är värdena samlade kring en linje med negativ lutning.
- Ingen korrelation: när observationsvärdena i spridningsdiagrammet inte följer någon linje alls
- Orsakssamband: ett samband där den ena variabeln är orsaken till att den andra förändras. Orsakssamband kallas ibland kausalitet. Korrelation visar bara samband men inte nödvändigtvis orsak.
- Regressionsanalys: utifrån korrelationen i ett spridningsdiagram vill vi beskriva sambandet med en linjär modell
- Linjär modell: är att beskriva ett samband genom att skapa en rät linje på formen \(f(x) = kx+m\)
