Andraderivatan
I det förra avsnittet, där vi gick igenom hur vi kunde bestämma karaktären av en funktions extremvärden utifrån en funktions derivata, såg vi hur vi kan avgöra om en punkt där funktionens derivata är noll är en extrempunkt (maximipunkt eller minimipunkt) eller en terrasspunkt. Vi gjorde detta genom att undersöka derivatans tecken i närliggande punkter.
Dock innebar denna metod en hel del räknearbete. Därför är det ju rimligt att undra om det inte finns något enklare sätt att komma fram till vilken typ av punkter det rör sig om, annat än att titta direkt på funktionens graf och försöka avgöra frågan därifrån (vilket inte alltid är en pålitlig metod).
Som tur är för oss finns det en metod som förenklar detta arbete en hel del.
Vi har tidigare lärt oss hur vi kan komma fram till ett uttryck för en funktions derivata utifrån en given funktion. Detta gjorde vi genom att följa de deriveringsregler som gått att härleda från derivatans definition.
Funktionens andraderivata får vi genom att derivera den ursprungliga funktionen två gånger. Vi kan använda andraderivatan för att t ex bestämma hur en kurva böjer sig, om en extrempunkt antar ett maximivärde eller minimivärde, hitta s k inflexionspunkter, och på så sätt konstruera grafer. I samtliga fall tittar vi på andraderivatans tecken eller teckenväxlingar kring en viss punkt.
Anta att vi har funktionen \(f(x) = 4x^2 +3x-6\) och med vill bestämma andraderivatan. Vi börjar då med att derivera funktionen första gången och får
$$f'(x) = 8x+3$$
Därefter deriverar vi en gång till och får
$$f''(x) = 8$$
Funktionens derivata (förstaderivata) till \(f(x)\) betecknas som vi sett \(f'(x)\). Följaktligen betecknas andraderivatan \(f''(x)\) och uttalas "f bis av x". Genom att använda andraderivatan kan vi alltså bl a avgöra hur en kurva böjer sig. Om det är en konvex eller konkav graf (kurva).
Exempel 1:
Bestäm andraderivatan \(f''(x)\) om
- \(f(x) = x^3+7x^2-x+2\)
- \(g(x) = x^2 -e^{2x}\)
Lösningar
- \(f(x)\) deriveras först en gång och vi får
$$f'(x)= 3x^2+14x-1$$
och så deriverar vi ytterligare en gång för att få
$$f''(x) = 6x+14$$
Svar: \(f''(x) = 6x+14\) - På liknande sätt deriveras \(g(x)\) två gånger,
$$g'(x) = 2x-2e^{2x}$$
och sedan
$$g''(x) = 2-2\cdot 2e^{2x} = 2-4e^{2x}$$
Svar: \(g''(x) =2-4e^{2x} \)
Konkav och konvex graf
Vi ska nu titta på hur vi kommer fram till att en funktion är konkav eller konvex.
Vi väljer för enkelhetens skull att studera två andragradsfunktioner.
Konkav graf
Betrakta figuren nedan som visar en andragradsfunktion \(f(x)\) med negativ parabel i ett intervall. Kännetecknande för en sådan är att koefficienten framför \(x^2\) termen är negativ.
På så sätt får funktionen också en global maximipunkt \(x = a\) i intervallet.
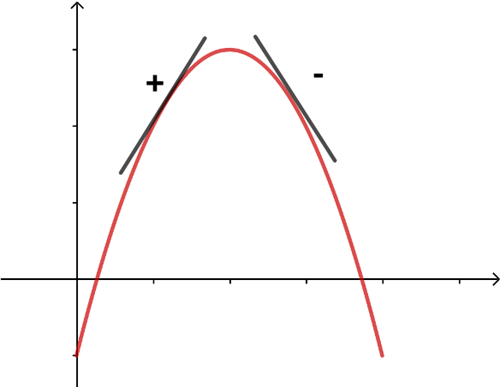
Vi ser att funktionen \(f(x)\) är strängt växande fram till maximipunkten \(x = a\) därefter strängt avtagande.
Det innebär att derivatan \(f'(x)\) är positiv fram till \(x = a\), precis vid \(x = a\) är \(f'(x) = 0\) och därefter är \(f'(x)\) negativ. Det betyder att \(f'(x)\), som ju är lika med tangenternas lutning, minskar i intervallet. Detta medför i sin tur att andraderivatan måste vara negativ dvs \(f''(x) < 0\) i intervallet. Den globala maximipunkten i intervallet uppträder där \(f'(x) = 0\) och \(f''(x) < 0\).
Vi ser att tangenterna ligger över grafen, då benämnes grafen konkav.
Konvex graf
I figuren nedan ser vi en andragradsfunktion med positiv parabel. Kännetecknande för en sådan är att koefficienten framför x2 termen är positiv. På så sätt får funktionen en global minimipunkt i intervallet.
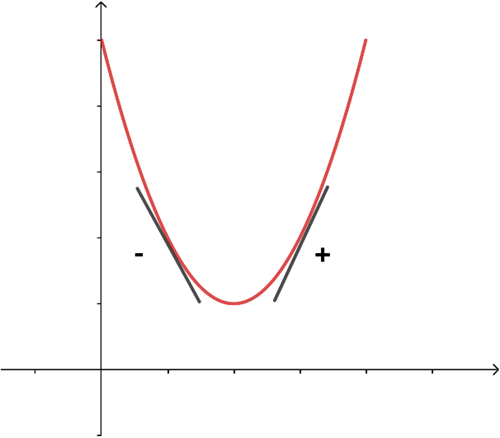
Vi ser att funktionen \(f(x)\) är strängt avtagande fram till \(x=a\) och därefter strängt växande.
Det innebär att derivatan \(f'(x)\) är negativ fram till \(x=a\), precis vid \(x=a\) är \(f'(x)=0\) och därefter är \(f'(x)\) positiv. Det betyder att \(f'(x)\), som ju är lika med tangenternas lutning, ökar i intervallet. Detta medför i sin tur att andraderivatan måste vara positiv dvs \(f''(x) > 0\) i intervallet. Den globala minimipunkten i intervallet uppträder där \(f'(x) = 0\) och \(f''(x) > 0\).
Vi ser att tangenterna ligger under grafen, då benämnes grafen konvex.
Inflexionspunkt
Grafen till en funktion \(f(x)\) kan se ut som figuren nedan visar. Funktionen är växande i intervallet \(0\leq x \leq 2\).
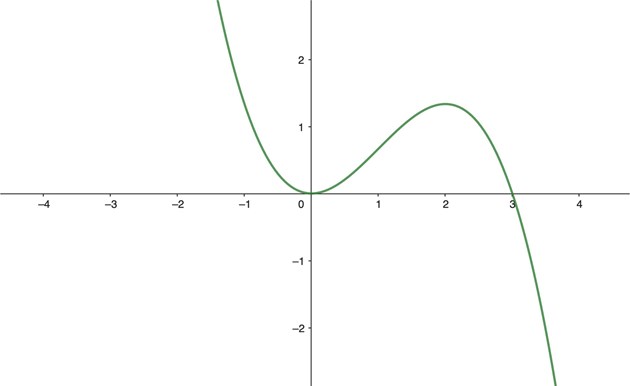
För att hålla reda på om grafen är konvex eller konkav kan vi dra sekanter längs grafen. Där sekanten hamnar under grafen, är grafen konkav. Där sekanten hamnar över grafen, är grafen konvex. Vi noterar också att funktionen har en s k inflexionspunkt där grafen övergår från att vara konkav till att bli konvex. Då funktionen övergår från att vara konkav till att bli konvex i inflexionspunkten, så byter också andraderivatan tecken från att vara negativ till att bli positiv. Det medför att andraderivatan \(f''(x) = 0\) i inflexionspunkten.
Viktigt att notera! För vissa funktioner kan \(f''(x) = 0\) utan att det är en inflexionspunkt. Då får vi studera teckenväxlingen vid den tänkta inflexionspunkten och även studera grafens utseende.
Exempel 2:
Funktionen \(f(x) = 2x^4-2x^3\) har inflexionspunkter. Bestäm koordinaterna för dessa punkter och bestäm de intervall där funktionen är konvex.
Lösning: Inflexionspunkter uppträder där andraderivatan är noll, \(f''(x) = 0\) så vi börjar med att bestämma \(f''(x)\)
$$f'(x) = 4\cdot 2x^3 -6x^2 = 8x^3-6x^2$$
$$f''(x) = 24x^2-12x$$
Vi bestämmer därefter andraderivatans nollställen
$$24x^2-12x = 0$$
$$x(24x-12)= 0$$
$$x_1=0$$
$$x_2 = \frac{1}{2}$$
Punkternas koordinater blir
$$f(0)=0$$
$$f(\frac{1}{2}) = 2\cdot {\left(\frac{1}{2}\right)}^4- 2\cdot {\left(\frac{1}{2}\right)}^3 = -\frac{1}{8}$$
Alltså \((0,0)\) och \(\left(\frac{1}{2},-\frac{1}{8}\right)\)
För att bestämma de intervall där funktionen är konvex gör vi en teckenstudie vid de tänkta inflexionspunkterna och tittar igen på andraderivatan \(f''(x)= 24x^2-12x\) och får
Om \(x<0 \rightarrow f''(x) \) blir positiv
Om \(x>\frac{1}{2} \rightarrow f''(x) \) blir positiv
Om \(0<x<0\frac{1}{2} \rightarrow f''(x) \) blir negativ
Vi har alltså teckenväxling på båda sidor om punkterna och de är då inflexionspunkter, vi ställer upp en teckentabell
| \(x\) | \(-1\) | \(0\) | \(\frac{1}{3}\) | \(\frac{1}{2}\) | \(1\) |
| \(f''(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | \(0\) | \(-\frac{1}{8}\) |
Vi har alltså teckenväxling på båda sidor om punkterna \(x= 0\) \(x= \frac{1}{2}\) och de är då inflexionspunkter.
Konvex graf får vi där \(f''(x)\) är positiv dvs för \(x<0\) och \(x>\frac{1}{2}\).
Svar:
Punkternas koordinater \((0,0)\) och \(\left(\frac{1}{2},-\frac{1}{8}\right)\)
Konvex graf för \(x<0\) och \(x>\frac{1}{2}\)
Lokala extrempunkter med hjälp av andraderivatan
Att få fram en funktions derivata kan gå till på följande sätt, utifrån de kända deriveringsreglerna, som tillämpas på en exempelfunktion:
$$f(x)=x^{3}-3x^{2}$$
Derivatan för denna tredjegradsfunktion är känd:
$$\\f'(x)=3x^{2}-6x$$
Vi identifierar x-värdena för möjliga extrempunkter genom att sätta derivatan lika med noll och sedan lösa ekvationen som uppkommer:
$$0=3x^{2}-6x\Rightarrow x_{1}=0,\: x_{2}=2$$
Eftersom vi hittade två x-värden, finns det två möjliga extrempunkter att undersöka.
Har vi funnit två punkter som är maximi-, minimi- eller terrasspunkter? Vi kan även i fortsättningen använda oss av teckenstudium, men den här gången ska vi testa en bättre metod:
Om vi deriverar uttrycket för funktionens derivata ytterligare en gång, då kommer vi fram till ett nytt uttryck som vi kallas funktionens andraderivata (därför att vi deriverat funktionen två gånger - funktionens derivata, alltså när vi bara har deriverat en gång, kallas även funktionens förstaderivata). Att derivera uttrycket för funktionens derivata följer samma deriveringsregler som vi tidigare använt:
$$\\f'(x)=3x^{2}-6x$$
$$\\f''(x)=6x-6$$
Uttrycket för funktionens andraderivata
$$f''(x)$$
uttalas "f bis x".
När vi nu har ett uttryck för denna funktions andraderivata kan vi sätta in våra tidigare funna x-värden i andraderivatan. Beroende på vilket värde vi får ut av andraderivatan för var och ett av dessa x-värden, kan vi dra olika slutsatser om huruvida punkterna är maximi-, minimi- eller terrasspunkter:
Är förstaderivatan lika med noll i en punkt, då är punkten en maximi-, minimi- eller terrasspunkt - vilken av dessa beror på värdet på andraderivatan enligt följande:
Maximipunkt
$$f''(x)<0$$
Om andraderivatan är negativ för det aktuella x-värdet är det ett maximivärde i punkten. vi säger att funktionen är konkav.
Minimipunkt
$$f''(x)>0$$
Om andraderivatan är positiv för det aktuella x-värdet är det ett minimivärde i punkten. vi säger att funktionen är konvex.
Terrasspunkt
Om funktionen har en terrasspunkt kommer:
$$f''(x)=0$$
Observera att andraderivatan kan vara lika med 0 i en extrempunkt utan att det är en terrasspunkt.
Vi tittar på följande exempel
$$f(x)=x^{4}$$
har ett extremvärde för x=0 vilket ger en andraderivata där:
$$f''(0)=0$$
Lägg märke till att extremvärdet för denna funktion inte är en terasspunkt, i det här fallet ger andraderivatan alltså inte tillräckligt med information om funktionens extremvärde. Slutsatsen vi kan dra av det här är att om vi får andraderivatan till 0 för en extrempunkt, måste vi göra en teckentabell för att avgöra om extrempunkten är ett lokalt maximi-, minimi- eller terrasspunkt.
Nu går vi tillbaka till tredjegradsfunktionen \( f(x)=x^{3}-3x^{2} \). Vi testar att sätta in de aktuella x-värdena i vår exempelfunktions andraderivata \( f''(x)=6x-6 \):
$$f''(0)=6\cdot 0-6=-6$$
$$f''(2)=6\cdot 2-6=6$$
Vi fick att andraderivatan blev -6 och 6, alltså kan vi säga att den första extrempunkten är ett lokalt maximivärde och den andra extrempunkten ett lokalt minimivärde.
Exempel 3:
Bestäm koordinaterna i de möjliga inflexionspunkterna för funktionen \(f(x) = 2x^4-3x^3+6\). Bestäm också i vilka intervall funktionen är konvex respektive konkav.
Lösning: Vi beräknar \(f''(x) = 0\) för att hitta möjliga inflexionspunkter
$$f'(x)= 8x^3-9x^2$$
$$f''(x)=24x^2-18x$$
$$24x^2-18x=6x(4x-3) =$$
$$x_1 = 0$$
$$x_2 = \frac{3}{4}$$
Vi beräknar koordinaterna direkt
$$f(0) = 6$$
$$f(\frac{3}{4}) = 5,37$$
Teckenstudie:
| \(x\) | \(-1\) | \(0\) | \(\frac{1}{2}\) | \(\frac{3}{4}\) | \(1\) |
| \(f(x)\) | \(6\) | \(5,37\) | |||
| \(f''(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| konvex | konkav | konvex |
Svar:
Koordinater inflexionspunkter: \((0,6)\) och \(\left(\frac{3}{4};5,37\right)\)
Konvex för \(x<0\) och \(x>\frac{3}{4}\)
Konkav för \(0<x<\frac{3}{4}\)
Sammanfattning:
Största eller minsta värde i ett intervall:
Lokala maximum eller minimum har inga större respektive mindre värden i närheten.
Största eller minsta värde för en funktion inom ett intervall uppstår i derivatans nollställen eller i intervallets ändpunkter om de tillhör definitionsmängden.
Konkav och konvex funktion samt inflexionspunkt:
Om \(f''(a)<0\), så är funktionen \(f(x)\) konkav kring \(x=a\).
Om \(f''(a)>0\), så är funktionen \(f(x)\) konvex kring \(x=a\).
Om funktionen \(f(x)\) har en inflexionspunkt för \(x=a\), så är \(f''(a) =0\).
Om \(f''(a) =0\) måste teckenväxling av \(f''(x)\) ske i \(x=a\) för att vara en inflexionspunkt.
Extrempunkter och extremvärden:
Om \(f'(x)=0\) och \(f''(a)<0\), så har funktionen en lokal maximipunkt för \(x=a\).
Om \(f'(x)=0\) och \(f''(a)>0\), så har funktionen en lokal minimipunkt för \(x=a\).
Om \(f'(x)=f''(x)=0\) , måste vi utföra teckenstudie av förstaderivatan för att avgöra typ av extrempunkt (maximipunkt, minimipunkt, eller terrasspunkt).
Här går vi igenom andraderivatan.
Här går vi igenom informationen andraderivatan ger oss.
- Derivata: en funktion som beskriver förändringshastigheten (lutningen) till en annan funktion
- Derivatans nollställen: vilka x-värden som löser ekvationen \(f’(x) =0\)
- Teckenstudie: en tabell där vi undersöker derivatans nollställen hur derivatan och själva funktionen beter sig kring dessa
- Maximipunkt: en punkt på grafen som utgör en vändpunkt, där grafen växer innan och avtar efter. På en parabel är detta det högsta värdet som grafen når, vid en maximipunkt är derivatan lika med noll
- Minimipunkt: en punkt på grafen som utgör en vändpunkt, där grafen avtar innan och växer efter. På en parabel är detta det minsta värdet som grafen når, vid en minimipunkt är derivatan lika med noll
- Terrasspunkt: en punkt på grafen som är som en platå, först växer grafen och sedan är den platt, (lutningen och derivatan är lika med noll) och sen växer den igen, eller först avtagande och platt och sen avtagande igen
- Extrempunkter: minimi- och maximipunkter är extrempunkter, det vill säga när derivatan är lika med 0
- Andraderivata: betecknas \(f’’(x)\) och uttalas ”f biss av x” och vi får det genom att derivera en funktion två gånger, dvs först derivera och sen hitta derivatan av funktionens derivata.
- Konkav graf: om andraderivatan har ett negativt värde för en punkt \(x=a\), dvs \(f’’(a) <0\) så är funktionen \(f(x)\) konkav kring punkten \(x=a\)
- Konvex graf: om andraderivatan har ett positivt värde för en punkt \(x=a\), dvs \(f’’(a) >0\) så är funktionen \(f(x)\) konvex kring punkten \(x=a\)
- Inflexionspunkt: när en funktion går från att vara konvex till konkav eller tvärtom, vi kan hitta inflexionspunkter då andra derivatan kommer vara lika med noll, \(f’’(x) = 0\)
