Komplexa talplanet

I det inledande avsnittet om komplexa tal skrev vi komplexa tal i rektangulär form, som \(z = a + bi\), där \(a\) och \(b\) är reella tal och \(i\) är den imaginära enheten.

I det här avsnittet ska vi undersöka några andra sätt att representera komplexa tal, via det komplexa talplanet.

Det komplexa talplanet

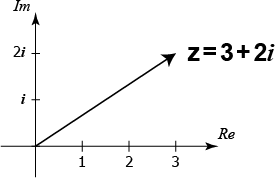
Om vi har ett reellt tal, till exempel \(x = 3\), så kan vi representera det som en position på tallinjen. Har vi på andra sidan ett komplex tal, till exempel \(z = 3 + 2i\), så räcker inte tallinjen till för att entydigt representera detta tal.

Istället får vi här lov att införa det komplexa talplanet, vilket vi kan åskådliggöra som ett koordinatsystem längs vars x-led vi anger det komplexa talets realdel (Re z) och längs vars y-led vi anger talets imaginärdel (Im z).

Härigenom kan vi i det komplexa talplanet representera ett komplex tal som antingen en punkt (Re z, Im z) eller som en pil från origo (0, 0) till en punkt (Re z, Im z).

Komplexa _tal __komplexa _talplanet _03

Addition och subtraktion i det komplexa talplanet

Det finns vissa likheter mellan hur vi kan representera komplexa tal i det komplexa talplanet med hur vi kan representera vektorer i ett rätvinkligt koordinatsystem.

Om vi adderar två komplexa tal, så kan vi representera det i det komplexa talplanet som att våra två komplexa tal uttrycks som pilar utgående från origo som utgör två av sidorna i ett parallellogram, och att summan av de båda komplexa talen utgörs av parallellogrammens diagonal utifrån origo.

Vi visar här hur en addition kan representeras i det komplexa talplanet, när vi adderar de båda komplexa talen z1 = -1 + 2i och z2 = 3 + i

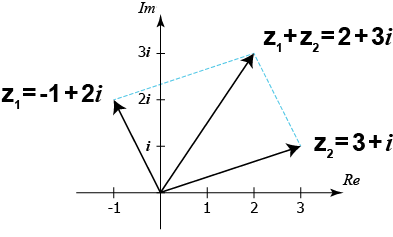
Komplexa _tal __komplexa _talplanet _04

Summan av de två komplexa talen blir alltså enligt räknereglerna för komplexa ta följande:

$${z}_{1}+{z}_{2}=(-1+2i)+(3+i)=$$

$$=-1+2i+3+i=$$

$$=2+3i$$

På motsvarande sätt utgör en subtraktion av två komplexa tal att vi till det första komplexa talet adderar minus det andra komplexa talet. Har vi till exempel differensen mellan de båda komplexa talen \(z_1 = -1 + 2i\) och \(z_2 = 3 + i\), alltså \(z_1 - z_2\), så motsvarar det \(z_1 + (-z_2)\).

Därför får vi

$${z}_{1}-{z}_{2}={z}_{1}+(-{z}_{2})=$$

$$=(-1+2i)+(-1)\cdot (3+i)=$$

$$=-1+2i-3-i=$$

$$=-4+i$$

I det komplexa talplanet motsvarar denna subtraktion följande:

komplexa tal och komplexa talplanet

Har du en fråga du vill ställa om Komplexa talplanet? Ställ den på Pluggakuten.se
Har du hittat ett fel, eller har du kommentarer till materialet på den här sidan? Mejla matteboken@mattecentrum.se

Genomgång av hur det komplexa talplanet är uppbyggt.

  • Imaginära enheten i: för att kunna hitta lösningar till negativa kvadratrötter infördes imaginära enheten \(i\) som har följande egenskaper:
    $$i^{2}=-1$$
    Som vi använder så här
    $$i=\sqrt{-1}$$
  • Komplext tal: ett tal som består av både en reell del och en imaginär del, rent allmänt betecknas det \(z = a+bi\)
  • Realdel: delen av ett komplex tal som består av enbart ett reellt tal. I \(z = a+bi\) är \(a\) realdelen. Betecknas ibland \(\Re (z)= Re(z) = a\)
  • Imaginärdel: delen av ett komplex tal som består av ett imaginärt tal. I \(z = a+bi\) är \(b\) imaginärdelen.  Betecknas ibland \(\Im (z) =Im (z)= b\)
  • Komplexa talplanet: ett koordinatsystem längs vars x-led vi anger det komplexa talets realdel \((Re (z))\) och längs vars y-led vi anger talets imaginärdel \((Im( z))\). I det komplexa talplanet kan vi representera ett komplex tal som antingen en punkt \((Re(z), Im(z))\) eller som en pil från origo \((0,0)\) till en punkt \((Re(z), Im(z))\).
  • Addition av komplexa tal: om vi adderar två komplexa tal \(z_1 = a + bi\) och \(z_2 = c + di\), så får vi

    $${z}_{1}+{z}_{2}=(a+bi)+(c+di)=$$

    $$=a+bi+c+di=$$

    $$=(a+c)+(b+d)i$$

  • Subtraktion av komplexa tal:om vi subtraherar två komplexa tal \(z_1 = a + bi\) och \(z_2 = c + di\), så får vi

    $${z}_{1}-{z}_{2}=(a+bi)-(c+di)=$$

    $$=a+bi-c-di=$$

    $$=(a-c)+(b-d)i$$