Integraler

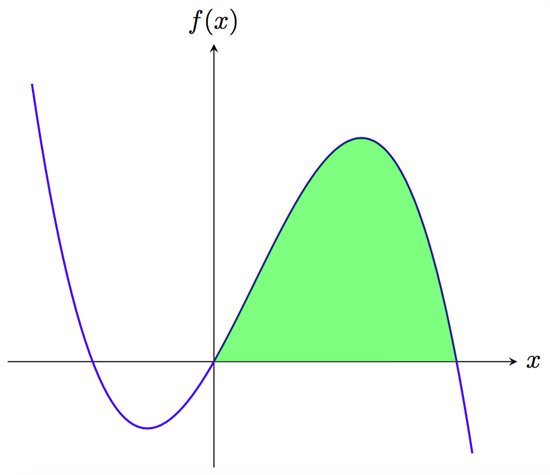
1. Bilden ovan visar kurvan \(y=-x^3+x^2+2x\). Bestäm var kurvan skär \(x\)-axeln. Bestäm även arean på det gröna området som avgränsas av kurvan och \(x\)-axeln.

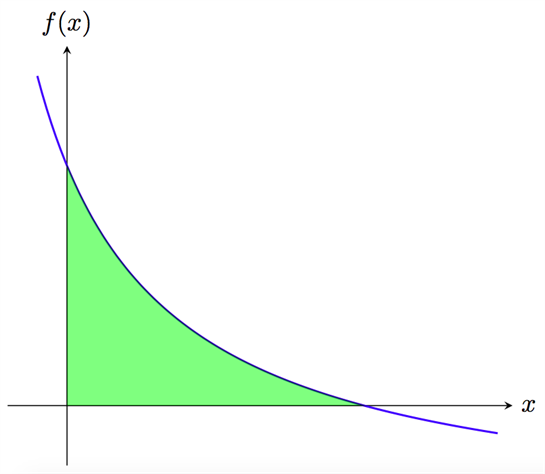
2. Bilden ovan visar en kurva \(f(x)\), som har den primitiva funktionen \(F(x)=3\cdot \ln(x+1)-x\). Bestäm först kurvan \(f(x)\) och sedan var den kurvan skär \(x\)-axeln. Bestäm även arean på det gröna området som avgränsas av kurvan och \(x\)-axeln.

Lösningsförslag:

1.

För att bestämma var kurvan skär \(x\)-axeln sätter vi \(y=0\) och löser den ekvationen:

$$y=-x^3+x^2+2x=0$$

Detta ger:

$$\begin{align}-x^3+x^2+2x & = 0 \\ -x(x^2-x-2) & = 0\end{align}$$

Här får vi fallindela och lösa två ekvationer:

Fall 1:

$$-x=0 \implies x=0$$

Här får vi första lösningen på var kurvan skär \(x\)-axeln, nämligen \(x_1=0\).

Fall 2:

$$x^2-x-2=0$$

Här använder vi pq-formeln:

$$\begin{align}x & =\frac{1}{2}\pm\sqrt{\left(\frac{1}{2}\right)^2+2} \\ x & = \frac{1}{2}\pm\sqrt{\frac{1}{4}+\frac{8}{4}} \\ x & = \frac{1}{2}\pm\sqrt{\frac{9}{4}} \\ x & = \frac{1}{2}\pm\frac{3}{2}\end{align}$$

$$\begin{align} x_2 & = 2\\ x_3 & = -1\end{align}$$

Vi har alltså hittat tre punkter då kurvan skär \(x\)-axeln, vilka är \(x_1=0\), \(x_2=2\) och \(x_3=-1\).

Nu ska vi räkna ut den grönfärgade arean. Arean beräknas med hjälp av integraler:

$$\begin{align} A & =\int_{0}^{2} -x^3+x^2+2x \\ & = \left[ -\frac{x^4}{4}+\frac{x^3}{3}+x^2\right]_{0}^{2} \\ & = \left( -\frac{2^4}{4}+\frac{2^3}{3}+2^2 \right)- \left(-\frac{0^4}{4}+\frac{0^3}{3}+0^2 \right) \\ & = \frac{8}{3}\end{align}$$

Det gröna området har alltså \( \frac{8}{3} \) area enheter.

2.

För att bestämma kurvan måste vi först derivera den primitiva funktionen \(F(x)\):

$$\begin{align} F(x) & = 3\cdot \ln(x+1)-x \\ F'(x) & = f(x) = \frac{3}{x+1}-1\end{align}$$

Vi ska nu hitta var kurvan skär \(x\)-axeln. För att göra det sätter vi \(f(x)=0\):

$$\begin{align} \frac{3}{x+1}-1 & = 0 \\ \frac{3}{x+1} & = 1 \\ 3 & = x+1 \\ x & = 2 \end{align}$$

Arean beräknas med hjälp av integraler:

$$\begin{align} A & = \int_{0}^{2} f(x) \, dx \\ & = F(2)-F(0) \\ & = ( 3\cdot \ln(2+1)-2 ) - ( 3\cdot \ln(0+1)-0 ) \\ & = 3\cdot \ln(3)-2 \end{align}$$

Det gröna området har alltså \( 3\cdot\ln(3)-2 \) area enheter.