Grafer
I det här kapitlet kommer vi att introducera det matematiska område som kallas grafteori, som handlar om att studera egenskaper hos grafer (ett begreppet som har en speciell innebörd i det grafteoretiska sammanhanget).
I detta inledande avsnitt går vi igenom grunderna vad gäller begreppet graf, för att i senare avsnitt studera vad vandringar, vägar och kretsar, samt stigar och cykler, i grafer är för något.
Begreppet graf inom grafteorin
När vi använder begreppet graf inom det matematiska området grafteori har det en annan betydelse än när vi tidigare talat om att t.ex. skissa en funktions graf i ett koordinatsystem.
En graf i det grafteoretiska sammanhanget består av två mängder, där elementen i den ena mängden (V) utgörs av grafens hörn och där elementen i den andra mängden (E) utgörs av de kanter som går mellan hörnen i V. Mängden V kan vi därför benämna grafens hörnmängd och mängden E kan vi benämna grafens kantmängd.
De termer som används inom det grafteoretiska området kan variera: vad vi här kallar hörn (engelska: vertices) kallas ibland även noder eller punkter, och vad vi kallar kanter (engelska: edges) kallas ibland bågar.
När man illustrerar en graf kan den till exempel se ut på följande sätt:
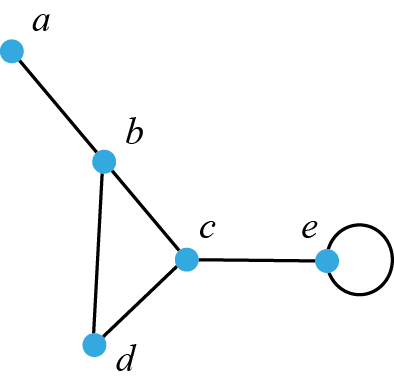
I bilden ovan är hörnen i grafen markerade med hjälp av punkter och bokstäverna a, b, c, d och e, och kanterna är markerade med linjer som sammanbinder hörn i grafen. Denna graf består av följande hörnmängd och kantmängd, där kanterna i kantmängden beskrivs med de par av hörn som kanten sammanbinder:
$$V=\{a,\,b,\,c,\,d,\,e\}$$
$$E=\{\{a,\,b\},\,\{b,\,c\},\,\{b,\,d\},\,\{c,\,d\},\,\{c,\,e\},\,\{e,\,e\}\}$$
Två hörn x och y (x ≠ y) kallas grannar om det går minst en kant mellan hörnen x och y. I den graf som vi skissade ovan har till exempel hörnet b grannarna a, c och d, eftersom kantmängden innehåller elementen {a, b}, {b, c} och {b, d}.
Vad hörnen och kanterna är tänkta att representera kan förstås variera beroende på sammanhang. Om vi till exempel studerar ett transportproblem kan hörnen utgöras av städer eller knutpunkter i trafiken, och kanterna utgöra de vägar eller andra kommunikationssätt som sammanbinder städerna/knutpunkterna. I ett sådant sammanhang kan vi till exempel vilja lösa problem av typen att ta reda på vilken som är den kortaste resvägen mellan två valfria städer eller den kortaste resväg som vi kan ta, om vi ska besöka en viss delmängd av städerna.
Att använda sig av illustrationer av grafer på det sätt som vi gjorde ovan fungerar bra när vi har att göra med relativt små grafer, men när antalet hörn och kanter ökar blir det snabbt opraktiskt att lösa problem utifrån illustrationen.
Skissa en bild av den graf som utgörs av följande hörnmängd och kantmängd.
$$V=\{a,\,b,\,c,\,d,\,e\}$$
$$E=\{\{a,\,b\},\,\{b,\,c\},\,\{c,\,d\},\,\{d,\,a\},\,\{c,\,e\},\,\{d,\,e\}\}$$
Vi börjar med att konstatera att vi har fem element i hörnmängden och sex element i kantmängden. Alltså ska vår bild innehålla fem hörn och sex kanter.
Undersöker vi kantmängden så ser vi att de fyra första kanterna binder samman hörnen a, b, c och d på ett sådant sätt att a har en kant gemensam med b, b har en kant gemensam med c, c har en kant gemensam med d, och d slutligen har en kant gemensam med a. Det här innebär att vi kan skissa denna del av grafen som en fyrhörning där fyrhörningens hörn utgörs av grafens hörn a, b, c och d:
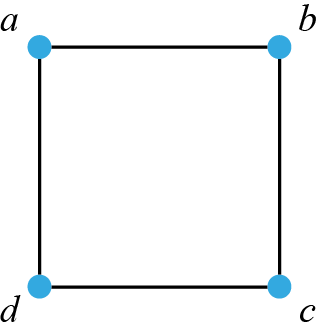
Därmed är vi klara med de fyra första kanterna i kantmängden. De två återstående kanterna i kantmängden, {c, e} och {d, e} sammanbinder hörnen c respektive d med hörnet e. Detta kan vi inkludera i vår skiss, genom att lägga till ett hörn e och låta denna punkt samt punkterna c och d utgöra hörnen i en triangel:
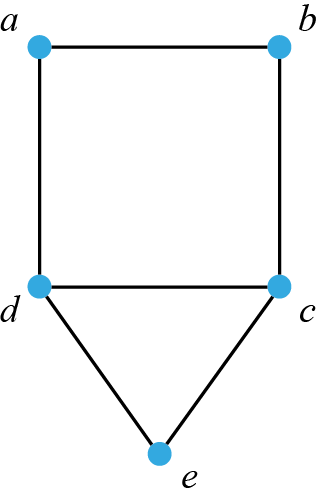
Nu har vi tagit med samtliga hörn i hörnmängden och samtliga kanter i kantmängden i vår skiss, och därmed är vi klara.
Hörn och kanter
En kant i en graf börjar i ett hörn och slutar i ett hörn. Därför kan vi med hjälp av den notation som vi introducerade i kapitlet om mängdlära beskriva en kant på följande sätt:
$$\{x,\,y\}\,\,\,d\ddot{a}r\,x\in V\,och\,y\in V$$
De hörn som kanten börjar och slutar i kan vara olika hörn eller samma hörn, det vill säga x ≠ y respektive x = y. Om en kant börjar och slutar i samma hörn kallar vi det en ögla eller loop. Ett exempel på en ögla har vi i den grafen som vi inledde avsnittet med, där vi har en kant {e, e}, som alltså både börjar och slutar i hörnet e.
I vissa sammanhang tillåter man att flera kanter går mellan samma par av hörn. Ett exempel där detta kan förekomma är med städer och vägar som går mellan städerna, där kan man tänka sig att det finns flera olika vägar som binder samman två städer.
Antalet kanter som är kopplade till ett hörn bestämmer hörnets grad eller valens. I grafen som vi inledde avsnittet med har hörnet a graden 1, hörnet d graden 2, och hörnen b, c och e graden 3 (hörnet e har graden 3, eftersom den har en kant gemensam med hörnet c och även en kant som börjar och slutar i hörnet e).
Om ett hörns grad är ett udda tal, säger vi att det är ett udda hörn; är hörnets grad ett jämnt tal, säger vi att det är ett jämnt hörn. Att kunna avgöra om hörn är udda eller jämna är användbart när vi analyserar förekomsten av så kallade Eulervägar och Eulerkretsar i grafer, vilket vi kommer att undersöka senare i detta kapitel.
