Trianglar
I tidigare avsnitt har vi lärt oss om olika typer av vinklar och om fyrhörningar.
I det här avsnittet ska vi lära oss om trianglar, olika typer av trianglar och hur vi beräknar en triangels omkrets och area.
Vad är en triangel?
En triangel är en geometrisk figur som har tre hörn. I vart och ett av hörnen har triangeln en vinkel och hörnen binds samman av tre sidor.
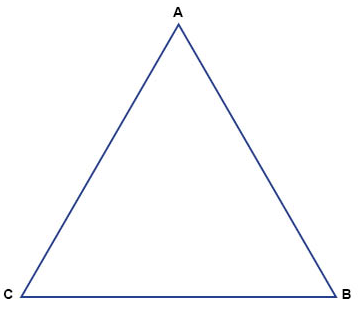
Hörnen i en triangel betecknar vi ofta med stora bokstäver (versaler), till exempel A, B och C som i bilden här ovanför. När vi säger en triangel ABC menar vi helt enkelt en triangel med hörnen A, B och C, och en sådan triangel betecknar vi ∆ABC. Ofta betecknar vi också vinkeln i ett hörn A som vinkel A.
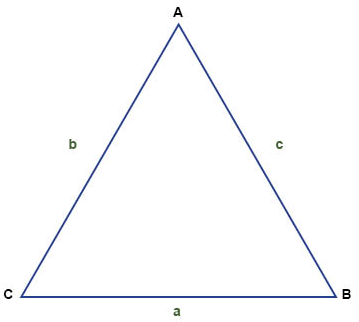
I en triangel gäller att en sida som befinner sig mittemot ett hörn A, kallas den motstående sidan, och betecknas med den lilla bokstaven (gemenen) som motsvarar hörnets beteckning. Till exempel är sidan som är motstående hörnet A en sida som vi betecknar a. Har vi en triangel ∆ABC så kan vi alltså beteckna dess sidor a, b och c.
Trianglars vinkelsumma (180°)
En viktig egenskap hos trianglar är att en triangels vinkelsumma är lika med 180°. Vinkelsumman får vi genom att vi adderar storleken på triangelns tre vinklar. Denna summa ska alltså alltid vara lika med 180°.
Har vi till exempel en triangel med vinklarna 80°, 70° och 30°, så blir vinkelsumman
$$ {80}^{\circ}+{70}^{\circ}+{30}^{\circ}={180}^{\circ}$$
Att vinkelsumman alltid ska vara lika med 180° kan vi använda oss av om vi till exempel vet hur stora två av triangelns vinklar är - då kan vi beräkna hur stor den tredje vinkeln måste vara. Den okända tredje vinkeln kan vi beräkna genom att från 180° subtrahera de båda kända vinklarna.
Beräkna storleken på den okända vinkeln
Två av vinklarna i en triangel är 60° respektive 70°.
Hur stor är då den tredje vinkeln i triangeln (den vinkel som betecknas v i figuren)?
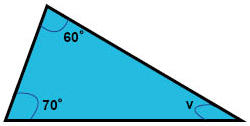
Eftersom vi vet att vinkelsumman i triangeln måste vara 180°, så kan vi teckna en ekvation för vinkelsumman, så här:
$$ {70}^{\circ}+{60}^{\circ}+v={180}^{\circ}$$
Vi har tidigare sett hur vi gör för att lösa en ekvation av den här typen. Vad vi vill göra är helt enkelt att hitta vilket värde på v som gör att ekvationens båda sidor blir lika.
Det gör vi genom att vi först förenklar den vänstra sidan, genom att addera de två kända vinklarna:
$$ {130}^{\circ}+v={180}^{\circ}$$
Den enda möjliga lösningen är att vinkeln v är lika med 50°, eftersom
$$ {130}^{\circ}+{50}^{\circ}={180}^{\circ}$$
Därför vet vi att den okända vinkeln v = 50°.
Olika typer av trianglar
Beroende på hur stora de olika vinklarna i en triangel är, kan vi del upp trianglar i olika typer. Vi ska titta på tre speciella typer av trianglar som förkommer ofta och är bra att känna till.
Rätvinkliga trianglar
En rätvinklig triangel är en triangel där en av vinklarna är en rät vinkel, det vill säga 90°.
I rätvinkliga trianglar är alltid den räta vinkeln den största vinkeln och summan av de båda andra vinklarna är 90°. I figuren ovan är vinkeln i hörnet A den räta vinkeln och summan av vinklarna i hörnen B och C måste vara 90°.
En annan intressant egenskap är att den sida i triangeln som är motstående den räta vinkeln, kommer att vara den längsta sidan i triangeln. I figuren ovan är vinkeln i hörnet A den räta vinkeln, så den längsta sidan i triangeln måste vara den motstående sidan, alltså sidan BC.
Likbenta trianglar
En likbent triangel är en triangel där två av sidorna är lika långa.
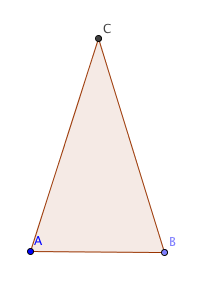
I figuren ovan är de båda sidorna AC och BC lika långa, så triangelns är likbent.
Att två av sidorna i triangeln är lika långa innebär också att två av triangelns vinklar är lika stora. I figuren ovan är det vinklarna i hörnen A och B som är lika stora. De båda vinklarna i en likbent triangel som är lika stora, kallar vi basvinklar.
Liksidiga trianglar
En liksidig triangel är en triangel där alla tre sidorna är lika långa.
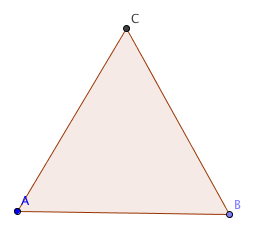
I figuren ovan är sidorna AB, AC och BC lika långa, så triangeln är liksidig.
Att triangelns tre sidor är lika långa innebär också att triangelns tre vinklar alla är lika stora. Eftersom summan av de tre lika stora vinklarna ska vara 180°, måste var och en av vinklarna vara 60°.
Omvänt gäller också att om vi har en triangel som har tre lika stora vinklar, då måste triangeln vara liksidig.
Trianglars omkrets
I avsnittet om fyrhörningar kom vi fram till att en fyrhörnings omkrets är lika med summan av längden på fyrhörningens fyra sidor.
På samma sätt kan vi beräkna en triangels omkrets som summan av längden på triangelns tre sidor. Betecknar vi sidorna med bokstäverna a, b och c, kan vi därför skriva triangelns omkrets, O, så här:
$$ O=a+b+c$$
Trianglars area
När vi ska beräkna en triangels area kan vi börja med att påminna oss om formeln för rektanglars area. En rektangels area är lika med basen multiplicerad med höjden:
$$ {A}_{rektangel}=b\cdot h$$
Om vi tänker oss att vi har en rektangel och sedan delar den längs diagonalen, då får vi två stycken rätvinkliga trianglar som är lika stora. Det kan vi se i figuren här nedanför.
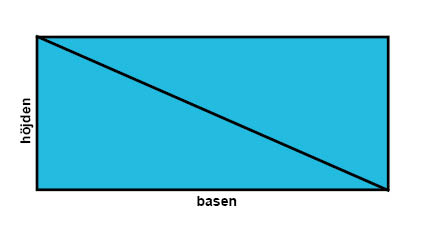
Arean av de rätvinkliga trianglarna ska ju tillsammans vara lika stor som rektangelns area, så därför måste var och en av de två rätvinkliga trianglarna ha arean
$$ {A}_{r\ddot{a}tvinklig\,triangel}=\frac{b\cdot h}{2}$$
där basen b och höjden h är vinkelbenen som går ut från den räta vinkeln.
Men det är inte alla trianglar som är rätvinkliga. Om vi har en triangel som inte är rätvinklig, då använder vi samma formel för att beräkna arean, men höjden h blir en annan.
$$ {A}_{triangel}=\frac{b\cdot h}{2}$$
Höjden h måste alltid vara vinkelrät mot basen b. Därför kan vi hitta höjden i triangeln så som vi visar i figuren här nedanför.
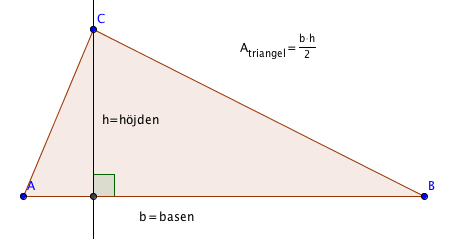
Beräkna omkrets och area för den här triangeln
Längden på sidorna står skrivna i cm.
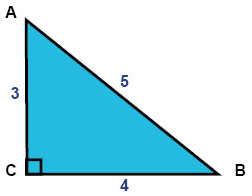
Vi vet att en triangels omkrets är lika med summan av längden på sidorna, så vi får den här omkretsen:
$$ {O}_{triangel}=5+4+3=12\,cm$$
I figuren kan vi se att vinkeln i hörnet C är en rät vinkel. Därför är triangeln rätvinklig. Det gör det enkelt att beräkna triangelns area.
Om vi låter sidan BC vara triangelns bas och sidan AC vara triangelns höjd, då kan vi beräkna triangelns area så här:
$$ {A}_{triangel}=\frac{b\cdot h}{2}=\frac{4\cdot 3}{2}=\frac{12}{2}=6\,{cm}^{2}$$
Alltså är triangelns omkrets 12 cm och triangelns area 6 cm2.
Videolektioner
I den här videon går vi igenom trianglar, vad det är och några viktiga egenskaper.
I den här videon går vi igenom tre olika typer av trianglar.
I den här videon ska vi gå igenom omkrets och area på trianglar.
I den här videon går vi igenom några viktiga begrepp som används för att beskriva en triangel.
