Vinklar

Att känna till hur vinklar fungerar kommer vi att ha stor användning för senare, bland annat när vi lär oss om fyrhörningar och trianglar.

Vinklar finns överallt

Om vi står vid botten av en uppförsbacke och funderar på hur olika branta backar kan vara, så kommer vi fram till att vissa backar är väldigt branta, medan andra backar inte alls är särskilt branta.

Men vad innebär det att en backe är brant? Om vi ser marken vid botten av backen som plan och sedan hur backen går uppåt, så kan vi tänka oss att det se ut ungefär så här:

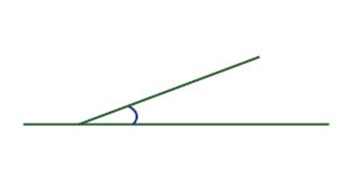
Vi kan se det som att det finns en vinkel mellan den horisontella marken och den branta backen. Den vinkeln är markerad i bilden här ovanför med en båge, som vi kallar en vinkelbåge.

Vinklar kan vi träffa på i många olika sammanhang. Om du ser dig omkring i ett vanligt rum kan du säkert hitta många vinklar, till exempel i hur två väggar möts i ett hörn eller hur brett isär två visare på en klocka står.

Vinklar

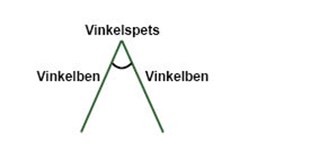
Den punkt som vinkeln utgår ifrån kallas vinkelspets. De två linjerna som möts i vinkelspetsen kallar vi vinkelben.

Vinklar mäter vi med enheten grader och markeras med symbolen °. Vill vi till exempel skriva en vinkel med storleken 45 grader, då kan vi skriva storleken på vinkeln som 45°. Ett helt varv (en cirkel) är uppdelat i 360°. Därför kan vi se 1° som

$$ \frac{1}{360}\,varv $$

Mäta en vinkel

Vinkelns storlek fås av hur många grader det krävs för att vrida det ena vinkelbenet, tills det täcker det andra. Det spelar ingen roll var på vinkelbenen vi mäter vinkeln eller hur långa vinkelbenen är, eftersom antalet grader alltid blir detsamma för en och samma vinkel.

För att mäta en vinkel kan vi använda en gradskiva. Vi placerar då gradskivans medelpunkt vid vinkelspetsen så som vi ser i bilden här nedanför. Det är viktigt att gradskivan är placerad så att det ena vinkelbenet pekar på gradtalet 0°. Sedan kan vi läsa av hur stor vinkeln är med hjälp av rätt skala på gradskivan.

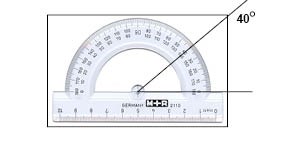
Ibland är den figur som vi mäter vinkeln i ganska liten och då kan vi förlänga vinkelbenen, så att det går att läsa av vinkelstorleken med hjälp av gradskivan. Längden på vinkelbenen påverkar ju inte hur stor vinkeln är, så det går bra att förlänga vinkelbenen hur mycket vi vill.

Rita en vinkel

När vi vill rita en vinkel på ett papper kan vi också använda en gradskiva.

Vi börjar då med att markera den punkt som vi vill ska vara vinkelspetsen. Från denna punkt ritar vi ut det ena vinkelbenet, så långt vi vill att det ska sträcka sig.

När vi har kommit så långt, placerar vi gradskivans mittpunkt i vinkelspetsen. Därefter ser vi till så att gradskivan är roterad så att det utritade vinkelbenet står där vinkeln är 0°.

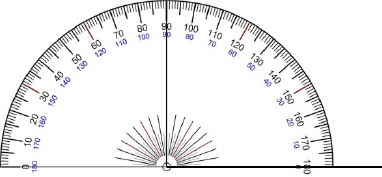
Sedan bestämmer vi hur stor vinkeln ska vara. Om vi till exempel vill rita en vinkel med storleken 50°, då läser vi av var på gradskivan 50° är och där gör vi en markering.

Det sista steget är att vi ritar ut en linje som binder ihop den markering vi nyss gjorde med vinkelspetsen.

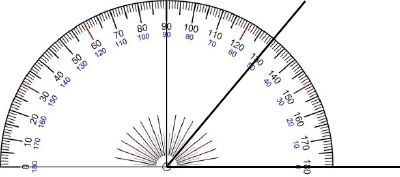
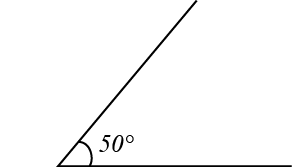
Nu har vi ritat en vinkel. Om vi vill vara extra tydliga, kan vi även rita ut en vinkelbåge, så att vi tydligt ser hur stor vinkeln är.

Olika typer av vinklar

För att göra det lättare att beskriva vinklar har man infört namn på olika typer av vinklar. Vi ska gå igenom några av de vanligaste typerna av vinklar och hur vi känner igen dem.

Namn	Beskrivning	Bild
Rät vinkel	En vinkel kallas rät om den är 90°. En rät vinkel motsvarar ett fjärdedels varv. I en figur markerar vi en rät vinkel med en liten kvadrat.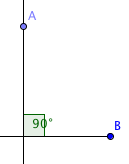
Spetsig vinkel	En vinkel kallas spetsig om den är mindre än en rät vinkel, alltså mindre än 90°.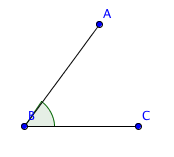
Trubbig vinkel	En vinkel kallas trubbig om den är större än en rät vinkel (90°), men samtidigt mindre än en rak vinkel (180°).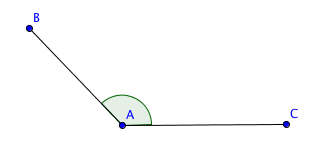
Rak vinkel	En vinkel kallas rak om den är dubbelt så stor som en rät vinkel, alltså att den är 180°, vilket är detsamma som ett halvt varv. För raka vinklar gäller att vinkelbenen är del av samma linje.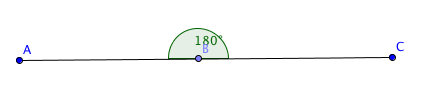
Konvex vinkel	En vinkel kallas konvex om den är större än en rak vinkel (180°), men samtidigt mindre än en hel vinkel (360°).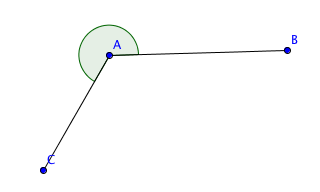
Hel vinkel	En vinkel kallas hel om den är 360°, det vill säga ett helt varv.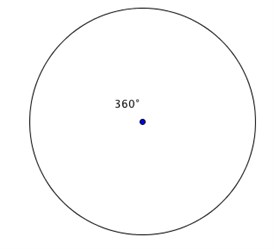

Videolektioner

I den här videon går vi igenom vinklar och några viktiga begrepp.

I den här videon går vi igenom fyra olika typer av vinklar: spetsig vinkel, rät vinkel, trubbig vinkel och konvex vinkel.

I den här videon går vi igenom vinklar.

I den här videon går vi igenom några olika vinklar.