Talet e
I Matte 2-kursen lärde vi oss att använda exponentialfunktioner. Exponentialfunktioner skrivs allmänt på formen:
$$f(x)=c\cdot a^{x}$$
där c och a är konstanter.
Ett exempel på en exponentialfunktion är
$$f(x)=2^{x}$$
I tidigare avsnitt har vi funnit deriveringsregler för ett antal vanliga polynomfunktioner. I detta avsnitt ska vi titta närmare på derivatan för en speciell typ av exponentialfunktion, nämligen den som innehåller talet e.
Kan en funktions derivata vara samma som funktionen?
Frågan vi ställer oss är alltså: finns det en funktion f(x) som har en derivata f'(x) som är lika med sig själv, med andra ord sammanfaller någonsin f(x)=f'(x)?
I följande figur har grafen till funktionen \(f(x) = 2^x \) och dess derivata \(f'(x) = 2^x \cdot 0,693 \) (mer om denna derivata i nästa avsnitt) ritats in. Lägg märke till hur lika funktionskurvan och derivatakurvan är varandra, det enda som skiljer dem åt är att derivatan multiplicerats med 0,693 och eftersom det är strax mindre än 1 så hamnar derivatakurvan strax under funktionskurvan.
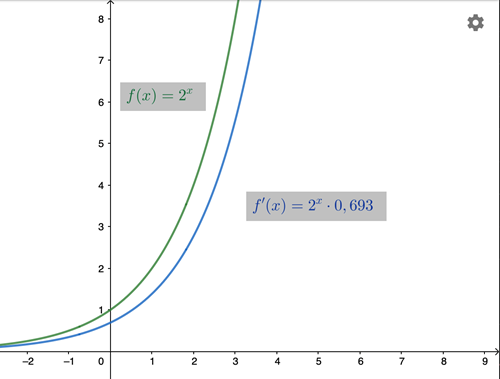
I följande figur har vi ritat in funktionen till \(y = 3^x \) samt dess derivata \( f '(x) = 3^x \cdot 1,099 \). Denna gång är värdet som derivatan multipliceras med strax över 1 och då hamnar derivatakurvan ovanför funktionskurvan, men även denna gång är kurvorna mycket lika varandra.
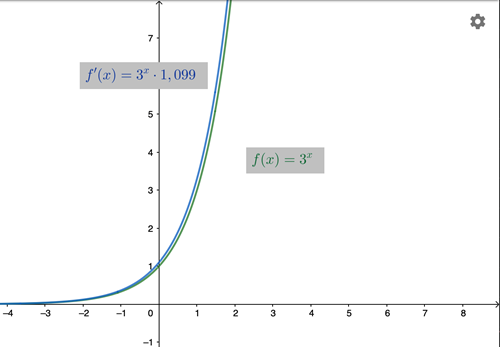
Frågan vi ställde oss själva i början kan omformuleras till: finns det någon exponentialfunktion, något värde på a så att \(f(x) = a^x= f'(x) \), där derivatans kurva helt sammanfaller med funktionens kurva? Från funktionerna vi undersökte innan förstår vi att \( a \) måste vara ett tal mellan 2 och 3. Vi fortsätter undersöka för vilken exponentialfunktion detta värde som multipliceras med derivatan blir just 1 och därför f(x) = f’(x)
| \(f(x)\) | \(f'(x)\) |
| \(2^x\) | \(2^x\cdot 0,693...\) |
| \(3^x\) | \(3^x\cdot 1,099...\) |
| \(2,9^x\) | \(2,9^x\cdot 1,066...\) |
| \(2,8^x\) | \(2,8^x\cdot 1,030...\) |
| \(2,7^x\) | \(2,7^x\cdot 0,993...\) |
| \(2,75^x\) | \(2,75^x\cdot 1,012...\) |
| \(2,72^x\) | \(2,72^x\cdot 1,0006...\) |
Svaret på frågan när f(x) är samma som f'(x) är när talet \(a\) i exponentialfunktionen är 2,71828..., men vi betecknar detta tal som \( e \) och funktionen blir:
$$f(x)=e^x$$
En sak att poängtera att värdet som \(a^x\) multipliceras med när det deriveras är \(\log_{e}(a)\) som kallas den naturliga logaritmen och betecknas oftast \(\ln(a)\), detta har varit närmevärdet vi använt och försökt få till. Vi kommer återkomma till den naturliga logaritmen i senare avsnitt, men vi kan ändå nämna att den blir enligt logaritmlagarna när \(\log_{e}(e) = \ln(e) = 1\). Därför blir derivatan av \(f(x)= a^x\) alltså \(f'(x) = a^x \cdot ln(a)\) och derivatan av \(f(x) = e^x\) blir därför \(f'(x) = e^x\cdot \ln(e) = e^x \cdot 1= e^x\).
Vi sammanfattar detta med deriveringsregeln
| \(f(x)\) | \(f'(x)\) |
| \(e^x\) | \(e^x\) |
Men var är detta tal e?
Talet e som vi får i funktionen är ett irrationellt tal , det betyder att e inte kan skrivas om som ett bråktal. Värdet på e är 2,718281828459045… och decimalerna fortsätter i oändligheten utan något särskilt mönster men ofta brukar vi använda avrundningen e ≈ 2,72. För att beräkna fler och fler decimaler av talet e används speciella datorer och i december 2020 slog en dator det senaste rekordet och beräknade e med 31415926535897 decimaler, det är 31 416 miljarder eller i grundpotensform \( \pi \cdot 10^{13}\).
Talet e kallas ibland Eulers tal efter den schweiziska matematikern Leonhard Euler, även om hans lärare använde talet ungefär 60 år innan Euler, men Euler var den första att beteckna talet med bokstaven e. Döpte han talet efter sitt eget namn, vad tror du?
Talet e uppkommer i ibland förvånande många områden i matematiken och går att definiera på många olika sätt. Vi kan visa med gränsvärde att
$$e = \lim_{h \to 0} {(1+h)}^{\frac{1}{h}} = \lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n $$
I sista steget byter vi \(h\) mot \(\frac{1}{n}\).
En av de mest användbara definitionerna av e är som bas till den naturliga logaritmen, som vi återkommer till i senare avsnitt.
- Exponentialfunktion: funktion med variabel i exponenten, skrivs på formen
$$ f(x) = C\cdot a^x $$
där C blir startvärde och a förändringsfaktor - Polynomfunktion: funktionen till ett polynom som har ekvationen på formen av ett algebraiskt uttryck med variabler och konstanttermer, där variablerna får endast ha exponenter som är positiva heltal. exempelvis är \(3x^2-4\) och \(-3x^7+0,8x^4-120\) polynom, medan \(x^{0,3}+4\) och \(5x^{-4}+x^2\) inte är det.
- Derivata: en funktion som beskriver förändringshastigheten (lutningen) till en annan funktion
- Derivatans definition: gränsvärdet när h närmar sig 0
$$ f’(x) = \lim_{h \to 0} = \frac{ f(x+h) -f(x)}{ h} $$ - Talet e: irrationellt tal som ungefär är lika med värdet 2,72… e är basen till den naturliga logaritmen och kan definieras med gränsvärdena
$$ e = \lim_{h \to 0} (1+h)^{\frac{1}{h}} = \lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n $$ - Gränsvärde: det värde som en funktion närmar sig när vi låter värdet vi stoppar in i funktionen närmar sig ett bestämt värde.
$$\lim_{x \to a} f(x)$$
”gränsvärdet av f(x) när x närmar sig a”
