Area Mellan Kurvor

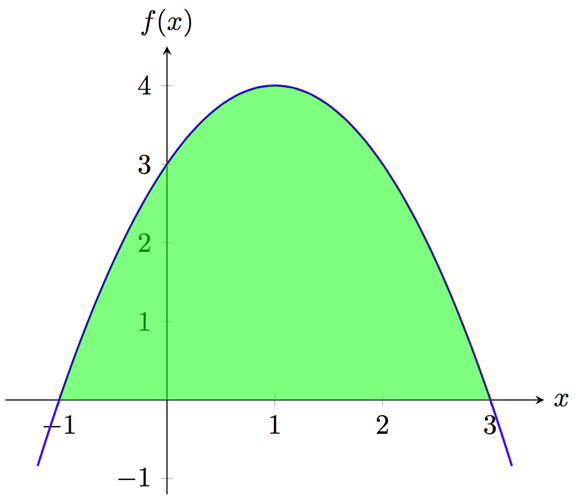
1 a. Bilden visar kurvan \(f(x) = -x^2+2x+3 \). Beräkna arean mellan kurvan och \(x\)-axeln (det gröna området).

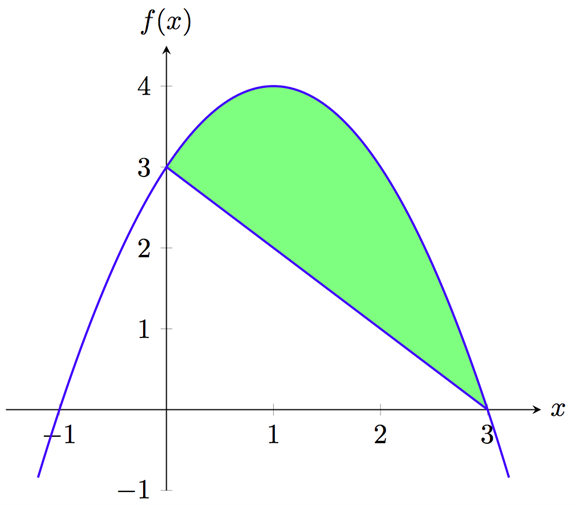
1 b. \((0,3)\) och \((3,0)\) är två punkter på kurvan \(f(x)=-x^2+2x+3\). Bestäm ekvationen för linjen som går igenom dessa två punkter. Beräkna sedan arean av området mellan kurvan och linjen (det gröna området).

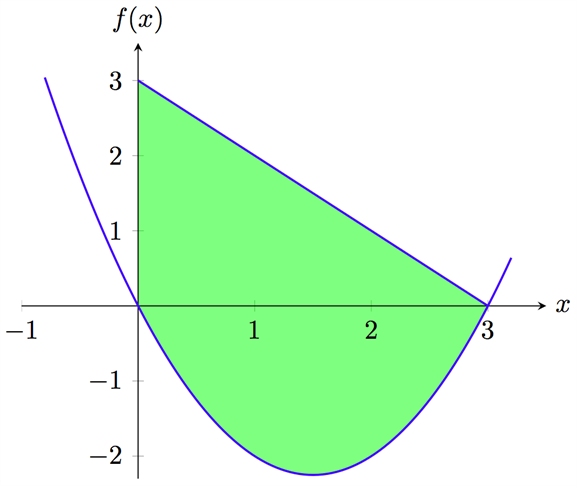
2 a. Bilden visar kurvan \(f(x)=x^2-3x\) och linjen \(y=-x+3\). Beräkna arean av området som begränsas av kurvan, linjen och \(y\)-axeln (det gröna området).

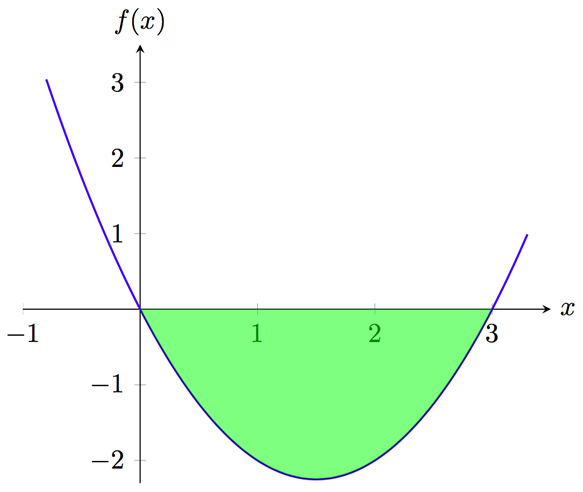
2 b. Beräkna arean för området som begränsas av kurvan \(f(x)=x^2-3x\) och \(x\)-axeln.

Lösningsförslag:

1 a.

För att räkna ut arean använder vi oss av integralberäkningar. På bilden ser vi att kurvan skär \(x\)-axeln i punkerna då \(x=-1\) och \(x=3\). Arean mellan \(x\)-axeln och kurvan \(f(x)=-x^2+2x+3\) är således:

$$\begin{align}A = & \int_{-1}^{3}(-x^2+2x+3) dx \\ = & \left[ -\frac{x^3}{3}+x^2+3x\right]_{-1}^{3} \\ = & \left( -\frac{3^3}{3}+3^2+3\cdot 3\right) - \left( - \frac{(-1)^3}{3}+(-1)^2+3\cdot(-1)\right) \\ = & (-3^2+3^2+3^2)- \left( \frac{1}{3}+1-3\right) \\ = & 9-\frac{1}{3}+2 \\ = & \frac{32}{3} \end{align}$$

Arean av det gröna området är alltså \(\frac{32}{3}\) area enheter.

1 b.

Ekvationen för linjen som går igenom punkterna \((0,3)\) och \((3,0)\) är av typen \(y=kx+m\). Vi får fram ekvationen genom att stoppa in punkterna i ekvationen och räknar ut \(k\) och \(m\):

$$\begin{align} 3 = & k\cdot 0+m \implies m=3 \\ 0 = & k\cdot3+3 \implies k=-1 \\ y = & -x+3 \end{align}$$

Linjens ekvation är alltså \(y=-x+3\). Arean mellan kurvan \(f(x) = -x^2+2x+3\) och linjen beräknas med hjälp av integralberäkning som vi lärde oss i Matte 3:

$$\begin{align} A = & \int_{0}^{3} (-x^{2}+2x+3) - (-x+3)dx \\ = & \int_{0}^{3} (-x^2+2x+3) dx - \int_{0}^{3} (-x+3)dx \\ = & \left [ -\frac{x^3}{3}+x^{2}+3x \right ]_{0}^{3}- \left[ -\frac{x^2}{2} +3x \right]_{0}^{3} \\ = & \left( -\frac{27}{3}+9+9 \right)-\left( -\frac{9}{2}+9\right) \\ = & 9-\frac{9}{2} \\ = & \frac{18}{2}-\frac{9}{2} \\ = & \frac{9}{2} = 4,5 \end{align}$$

Arean av det gröna området är således 4,5 area enheter.

2 a.

Arean av området som begränsas av kurvan \(f(x) = x^2 - 3x\), linjen \(y = -x+3\) och \(y\)-axeln beräknas på samma sätt som i uppgift 1 b, alltså:

$$\begin{align} A = & \int_{0}^{3} (-x+3)-(x^2-3x) dx \\ = & \int_{0}^{3} (-x+3) dx - \int_{0}^{3} (x^2-3x) dx \\ = & \left[ -\frac{x^2}{2}+3x \right]_{0}^{3}- \left[\frac{x^3}{3}-\frac{3x^2}{2}\right]_{0}^{3} \\ = & \left( -\frac{9}{2}+9\right) - \left( \frac{27}{3}-\frac{27}{2}\right) \\ = & \frac{9}{2}-\left( -\frac{27}{6}\right) \\ = & \frac{9}{2}+\frac{27}{6} \\ = & \frac{27}{6}+ \frac{27}{6} \\ = & \frac{27}{3} = 9 \end{align}$$

Arean av det gröna området är således 9 area enheter.

2 b.

Arean av detta område beräknas genom integralen:

$$\begin{align} A = & \int_{0}^{3}(x^{2}-3x)dx \\ = & \left[ \frac{x^{3}}{3}-\frac{3x^2}{2} \right]_{0}^{3} \\ = & \left( \frac{3^{3}}{3}-\frac{3\cdot3^2}{2} \right) - \left( \frac{0^{3}}{3}-\frac{3\cdot 0^2}{2}\right) \\ = & \frac{27}{3}-\frac{27}{2} \\ = & -\frac{27}{6} \\ = & -4,5 \end{align}$$

Arean av det gröna området är således 4,5 area enheter.