Klot, kon och pyramid
I det här avsnittet lär vi oss beräkna volymen och arean av ett klot, koner och pyramider.
Klot/sfär
Ett klot eller en sfär är en tredimensionell kropp som har formen av en boll. Dess yta kallas för klotyta och den cirkel som går runt mitten på klotet dvs har avståndet till klotets medelpunkt som radie, kallas för storcirkel. Klotytan är den avgränsningsyta som omger klotet.

Arean för ett klot beräknas enligt formeln:
$$A_{\text{klot}}=4\cdot \pi \cdot r^{2}$$
Volymen för ett klot beräknas enligt formeln:
$$V_{\text{klot}}=\frac{4\cdot \pi \cdot r^{3}}{3}$$
Kon
En kon utgörs av en basyta och en mantelyta. Mantelytan bildas genom att punkter längs basytans ytterkant förbinds med en punkt som ligger ovanför basytan. Bland koner är den vanligast förekommande det som kallas för en rak cirkulär kon. Den kallas så för att basytans kant har formen av en cirkel, och för att konens spets ligger centrerat över basytans mittpunkt.
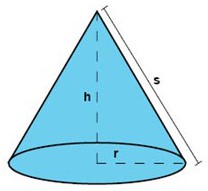
En kon har en volym som är en tredjedel av volymen av en cylinder som har samma basarea och höjd. Formeln för volymen av en rak cirkulär kon blir därför:
$$V_{\text{kon}}=\frac{\pi \cdot r^{2}\cdot h}{3} $$
Mantelytans area beräknas genom följande formel:
$$\text{Mantelarea}_{\text{kon}} = \pi\cdot r\cdot s=\pi\cdot r\cdot \sqrt{r^2+h^2}$$
Där \(s\) är sträckan mellan konens högsta punkt och kanten på basytan, som man kan beräkna med hjälp av Pythagoras sats om man vet konens höjd och radie.
Pyramid
En pyramid ett specialfall av en kon, där basytan har formen av en månghörning (även kallat polygon).
Eftersom pyramider är ett gemensamt begrepp för dessa objekt, oavsett hur många hörn basen har, leder det till att pyramider kan ha väldigt olika utseenden. Men de vanligast förekommande har en bas i form av en triangel eller en kvadrat.

På samma sätt som konens volym är proportionell till en cylinders volym, är pyramidens volym proportionell till ett prismas volym. Pyramidens volym är en tredjedel av volymen för ett prisma med samma höjd och area. Volymen beräknas enligt följande formel, där B står för basytans area.
$$V_{\text{pyramid}}=\frac{B\cdot h} {3}$$
Här går vi igenom hur vi beräknar volymen och arean för ett klot.
Här går vi igenom hur vi beräknar volymen och arean av en rak cirkulär kon.
Hjälpmedel
Här används grafräknaren Casio FX-CG20.
Se samma uppgift med grafräknaren Casio FX-9750GII.
Grafräknare av andra fabrikat har ungefär motsvarande funktionalitet.
- Klot/Sfär: Det tredimensionella objektet i form av en rund boll, vars motsvarighet i två dimensioner är en cirkel. Viktigaste måttet vid beräkningar med klot är dess radie.
$$A_{klot}=4\cdot \pi \cdot r^{2}$$$$V_{klot}=\frac{4\cdot \pi \cdot r^{3}}{3}$$ - Tredimensionell: Något som befinner sig i rummets samtliga tre dimensioner. T ex en kub, eller en cylinder.
- Kon: En spetsig tredimensionell kropp, som har en rund basyta och någon höjd. Om konen är en rak cirkulär kon, beräknas volymen genom
$$V_{\text{kon}}=\frac{\pi \cdot r^{2}\cdot h}{3} $$ - Pyramid: En spetsig tredimensionell kropp som har en mångsidig basyta och en viss höjd h. Volymen beräknas genom följande formel, där B är basytans area
$$V_{\text{pyramid}}=\frac{B\cdot h} {3}$$ - Polygon: Det formella ordet för en månghörning.
