Omkrets och area

Omkrets används för att bestämma hur långt det är runt en figur och area används för att mäta ytan av en figur. I det här avsnittet tittar vi på hur man tar fram omkrets och area för några vanliga figurer inom matematiken. Vi tittar också på hur man omvandlar area mellan olika enheter.

Omkrets

En figurs omkrets är den sammanlagda längden av de linjer eller kurvor som avgränsar figuren.

Fyrhörningar

Fyrhörningar har alltid fyra sidor. Om man summerar längden på dessa fyra sidor får man fyrhörningens omkrets. Nedan ser vi några av de vanligare fyrhörningarna.

Parallellogram

En parallellogram har fyra sidor och dess motstående sidor är parallella och lika långa.

Rektangel

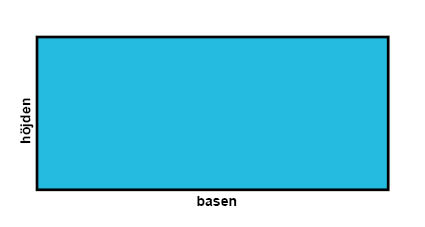
En rektangel är ett specialfall av en parallellogram, men som enbart har räta vinklar. Det innebär att alla rektanglar även är parallellogram. Motstående sidor är lika långa.

Kvadrat

En kvadrat är ett specialfall av en rektangel, men där alla sidor har samma längd. Eftersom alla kvadrater är rektanglar är de också parallellogram.

Triangel

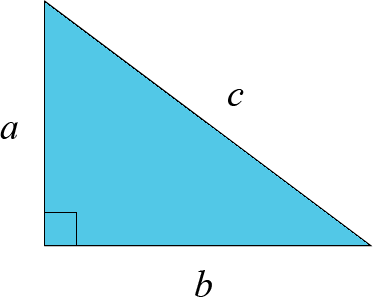
Trianglar har alltid tre sidor. Omkretsen av en triangel är summan av dess tre sidor.

Cirkel

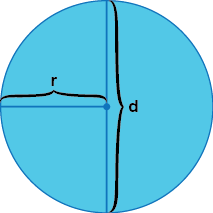
Om vi dividerar en cirkels omkrets med dess diameter \(d\) kommer vi alltid att få samma förhållande, oavsett cirkelns storlek. Förhållandet är \(\pi\), uttalas pi, och är ungefär \(3,14\).

Omkretsen blir då \(\pi\) multiplicerat med diametern \(d\), alltså:

$$\text{omkrets}=\pi\cdot d$$

Area

Area är ett mått på hur stor en yta är. Hur man räknar ut arean beror på figuren, nu ska vi titta på hur man räknar ut arean för några vanliga figurer.

Kvadrat, rektangel och parallellogram

Arean för en kvadrat, rektangel, eller parallellogram följer alla samma formel:

$$Arean=basen\cdot höjden$$

Vilket ofta brukar skrivas som

$$A=b\cdot h$$

För kvadrater och rektanglar gäller att basen, b, utgör den ena sidan, medan höjden, h, utgör en av de sidor som ligger intill basen. Vanligtvis väljer man basen som den sida som ligger nederst i en kvadrat eller rektangel, horisontellt, och höjden till en av figurens vertikala sidor. För parallellogram gäller att basen är en av figurens sidor och höjden utgörs av det vinkelräta avståndet mellan basen och motstående sida, se figur nedan.

Triangel

Arean för en triangel får man enligt följande formel

$$A_{triangel}=\frac{basen\cdot höjden}{2}=\frac{b\cdot h}{2}$$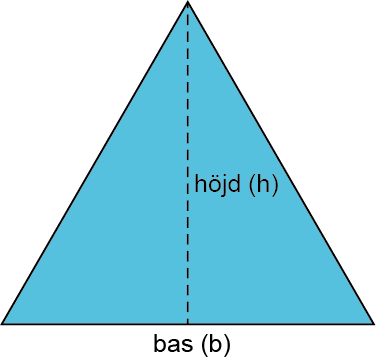

Cirkel

Arean av en cirkel får man genom följande formel:

$$A_{cirkel}=\pi \cdot r^{2}$$

Där \(r\) är cirkelns radie.

Enheter

En ytas area mäts alltid i kvadratenheter. Kvadratenheten kan till exempel vara kvadratmeter. En kvadratmeter är arean av en kvadrat med sidan en meter och skrivs \(1\;m\cdot1\;m=1\;m^2\). Andra enheter är t.ex. kvadratdecimeter, kvadratcentimeter och kvadratmillimeter som skrivs \(dm^2\), \(cm^2\) respektive \(mm^2\).

Enheter för area kan omvandlas på följande sätt:

$$1\;m^2 = 10\;dm\cdot10\;dm=10^2\;dm^2=100\;dm^2$$

$$1\;dm^2 = 10\;cm\cdot10\;cm=10^2\;cm^2=100\;cm^2$$

$$1\;cm^2 = 10\;mm\cdot10\;mm=10^2\;mm^2 =100\;mm^2$$

Omvandling:

$$m^2 \rightarrow dm^2\; \text{multiplicerar med}\;10^2$$

$$cm^2 \rightarrow mm^2\; \text{multiplicerar med}\;10^2$$