Area
Tidigare har vi pratat om längder och omkresten av geometriska figurer. Nu ska vi tala om arean. När en vägg ska målas eller tapetseras är det inte så viktigt att veta omkretsen. Det är viktigare att veta hur stor ytan är, alltså arean.
En kvadrat vars sidor är 1 cm säger vi har arean 1 kvadratcentimeter. Detta skrivs 1 cm2.
Den är ungefär såhär stor:
För större ytor används dm2, m2 eller km2.
Olle får frågan hur stor följande rektangel är.
Därför vill han räkna ut figurens area. Han kan göra det genom att fylla den med en kvadratcentimeter stora kvadrater och räkna hur många som får plats.
Sammanlagt 12 rutor. Alltså är arean 12 cm2.
Eftersom vi vet sidornas längd så kan vi beräkna arean på ett snabbare sätt. Det räcker med att räkna sida \( \cdot \) sida, alltså:
$$3\cdot4=12$$
Svar: Rektangelns area är 12 cm²
Två figurer kan ha samma omkrets men olika area. Area och omkrets är alltså inte samma sak.
Arean av en triangel
I varje triangel kan vi mäta upp en höjd och en bas.
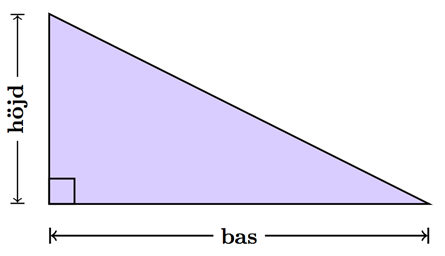
Vi kan skapa en rektangel med samma mått genom att lägga en kopia av triangeln bredvid sig själv:
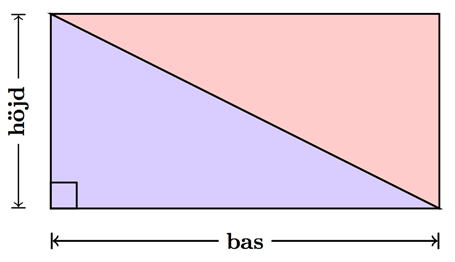
Det betyder att triangelns area är precis hälften av arean av en rektangel som har samma mått!
$$Rektangelns\: area=bas \cdot höjd$$
$$Triangelns\: area=\frac{bas \cdot höjd}{2}$$
Beräkna arean av följande triangel
$$\frac{4\cdot 6,5}{2}=\frac{26}{2}=13\: cm^{2}$$
Svar: 13 cm²
Beräkna arean av följande triangel:
När triangeln inte har någon rät vinkel måste vi mäta höjden på ett annat sätt än det vi gjorde tidigare. Höjden mäter vi genom att dra ett streck från basen upp till den högsta toppen. Det är viktigt att det nya strecket har en rät vinkel mot basen. Nu kan vi mäta med en linjal och få ut att höjden är 7 cm.
$$\frac{5,7\cdot 7}{2}=\frac{35+4,9}{2}=\frac{39,9}{2}=19,95\: cm^{2}$$
Svar: 19,95 cm²
