Addition och subtraktion av bråk

I det här avsnittet ska vi undersöka hur vi gör då vi vill addera eller subtrahera tal skrivna i bråkform.

Addition av bråk med gemensamma nämnare

Ju fler lika stora delar något har delats upp i, desto mindre del av det hela utgör varje del. Det här kan ställa till problem för oss när vi ska addera eller subtrahera bråktal, eftersom till exempel 1/3 är mer än 1/4.

Om vi först tittar på bråktal som har gemensamma nämnare, det vill säga att bråktalen har samma värde i sina nämnare, då ser vi att det går bra att addera dem, eftersom nämnarna är lika stora och delarna därför är jämförbara.

Vad vi gör i detta fall är att vi skriver summan på ett gemensamt bråkstreck genom att vi adderar täljarna i bråktalen och behåller deras gemensamma nämnare som den är.

---

Som ett exempel på detta har vi två bråktal med den gemensamma nämnaren 5, som går att addera direkt

$$ \frac{1}{5}+\frac{2}{5}$$

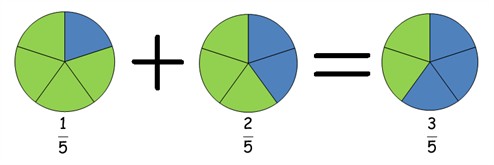
När vi beräknar summan av de båda bråktalen får vi det här:

$$ \frac{1}{5}+\frac{2}{5}=\frac{1+2}{5}=\frac{3}{5}$$

I det här exemplet var det alltså lätt att addera de båda bråktalen, eftersom de hade samma nämnare.

---

Subtraktion av bråk med gemensamma nämnare

På samma sätt som vi gjorde när vi adderade bråktal som har gemensamma nämnare kan vi göra om vi vill subtrahera. I sådana fall skriver vi differensen på ett gemensamt bråkstreck genom att vi subtraherar täljarna i de båda bråktalen och behåller deras gemensamma nämnare som den är.

Här har vi ett exempel på subtraktion av bråk med gemensamma nämnare:

$$ \frac{3}{5}-\frac{2}{5}=\frac{3-2}{5}=\frac{1}{5}$$

---

Beräkna värdena av dessa uttryck

Svara i enklaste form.

1. $$\frac{4}{7}+\frac{2}{7}$$
   Vi ser att de båda termerna har gemensam nämnare (7). Det betyder att vi kan räkna ut summan genom att addera täljarna (4 och 2) och låta nämnaren vara oförändrad. Därför får vi det här:

   $$ \frac{4}{7}+\frac{2}{7}=\frac{4+2}{7}=\frac{6}{7}$$

   Summan av 4/7 och 2/7 är alltså 6/7. Vi kan inte skriva om 6/7 i någon enklare form, så vi är klara med uppgiften.

   ---

2. $$\frac{5}{6}-\frac{3}{6}$$
   I den här uppgiften har de båda termerna gemensam nämnare (6). Därför kan vi skriva differensen på ett gemensamt bråkstreck genom att vi subtraherar täljarna (5 och 3) och låter nämnaren vara oförändrad. Vi får den här differensen:

   $$ \frac{5}{6}-\frac{3}{6}=\frac{5-3}{6}=\frac{2}{6}$$

   Differensen mellan 5/6 och 3/6 är alltså 2/6.

   Är bråktalet 2/6 skrivet i sin enklaste form? Nej, det är det inte, eftersom vi kan dividera både täljaren (2) och nämnaren (6) med 2. Därför förkortar vi bråktalet med 2, vilket ger oss det här:

   $$ \frac{2}{6}=\frac{\,\,\frac{2}{{\color{Red} 2}}\,\,}{\frac{6}{{\color{Red} 2}}}=\frac{1}{3}$$

   Vad vi kommit fram till nu är differensen skriven i sin enklaste form, 1/3. Differensen mellan 5/6 och 3/6 är alltså 1/3.

---

Addition av bråk med olika nämnare

Hur gör vi om vi vill addera bråktal som har olika nämnare?

Om de båda bråktalen har olika nämnare, då får vi först skriva om talen, så att de har gemensam nämnare.

För att skriva om bråktalen så att de får gemensam nämnare, använder vi oss av förkortning och förlängning.

Till exempel kan vi vilja beräkna den här summan av två bråktal:

$$ \frac{1}{4}+\frac{1}{3}$$

Vi kan direkt se att de båda termerna har olika nämnare: den först termen har nämnaren 4 och den andra termen har nämnaren 3. Därför behöver vi skriva om bråktalen, så att de står skrivna med gemensam nämnare.

Det enklaste sättet att hitta en gemensam nämnare för två bråktal, är att multiplicera de båda bråktalens nämnare med varandra. Produkten av nämnarna ska då bli den nya nämnaren:

$$ 4\cdot 3=12$$

Vi vill alltså skriva om de båda bråken, så att de står skrivna som tolftedelar istället för som fjärdedelar respektive tredjedelar. En fjärdedel är detsamma som tre tolftedelar, så vi förlänger bråket 1/4 med 3 och får då det här:

$$ \frac{1}{4}=\frac{1\,{\color{Red} {\cdot \,3}}}{4\,{\color{Red} {\cdot \,3}}}=\frac{3}{12}$$

Nu har vi skrivit om 1/4 som 3/12.

På samma sätt kan vi göra med 1/3, men här ska vi förlänga med 4 eftersom:

$$ 3\cdot 4 =12$$

Förlänger vi 1/3 med 4 så får vi det här:

$$ \frac{1}{3}=\frac{1\,{\color{Red} {\cdot \,4}}}{3\,{\color{Red} {\cdot \,4}}}=\frac{4}{12}$$

Nu har vi alltså skrivit om 1/3 som 4/12.

Eftersom de båda bråktalen nu är skrivna som tolftedelar har de gemensam nämnare (12).

$$ \frac{1}{4}+\frac{1}{3}=\frac{3}{12}+\frac{4}{12}$$

Därför kan vi nu beräkna deras summa genom att addera täljarna. Summan blir därför

$$ \frac{3}{12}+\frac{4}{12}=\frac{3+4}{12}=\frac{7}{12}$$

Summan av 1/4 och 1/3 är alltså lika med 7/12.

Subtraktion av bråk med olika nämnare

På samma sätt som vi gjorde när vi skulle addera två bråktal med olika nämnare, behöver vi skriva om bråktalen om vi ska subtrahera två bråktal med olika nämnare.

Till exempel kan vi vilja beräkna den här differensen:

$$ \frac{4}{5}-\frac{2}{3}$$

Först får vi skriva om de båda bråktalen, så att de har en gemensam nämnare. Den gemensamma nämnaren blir i det här fallet 15, eftersom produkten av termernas nämnare (5 och 3) blir 15:

$$ 5\cdot 3=15$$

När vi nu vet vilken gemensam nämnare vi vill ha, skriver vi om de båda bråktalen, så att de står skrivna som femtondelar. Den första termen får vi förlänga med 3 för att nämnaren ska bli 15. Därför får vi det här:

$$ \frac{4}{5}=\frac{4\,{\color{Red}{ \cdot \,3}}}{5\,{\color{Red} {\cdot \,3}}}=\frac{12}{15}$$

4/5 kan vi alltså skriva som 12/15.

Den andra termen får vi förlänga med 5 för att nämnaren ska bli 15. Därför får vi detta:

$$ \frac{2}{3}=\frac{2\,{\color{Red}{ \cdot \,5}}}{3\,{\color{Red} {\cdot \,5}}}=\frac{10}{15}$$

Nu vet vi att vi kan skriva 2/3 som 10/15.

När de båda termerna nu står skrivna som femtondelar kan vi subtrahera dem:

$$ \frac{4}{5}-\frac{2}{3}=\frac{12}{15}-\frac{10}{15}=\frac{12-10}{15}=\frac{2}{15}$$

Vad vi har kommit fram till nu är alltså att differensen mellan 4/5 och 2/3 är lika med 2/15.

---

Beräkna värdena av dessa uttryck

Svara i enklaste form.

1. $$\frac{1}{6}+\frac{2}{5}$$
   Eftersom termerna har olika nämnare (6 och 5), får vi skriva om bråktalen med gemensam nämnare. En sådan gemensam nämnare är

   $$ 6\cdot 5=30$$

   Därför förlänger vi bråktalet 1/6 med 5 och bråktalet 2/5 med 6. Vi får:

   $$\frac{1}{6}=\frac{1\,{\color{Red} {\cdot \,5}}}{6\,{\color{Red} {\cdot \,5}}}=\frac{5}{30}$$

   $$\frac{2}{5}=\frac{2\,{\color{Red} {\cdot \,6}}}{5\,{\color{Red} {\cdot \,6}}}=\frac{12}{30}$$

   Summan av de båda bråktalen kan vi därför skriva så här:

   $$ \frac{1}{6}+\frac{2}{5}=\frac{5}{30}+\frac{12}{30}$$

   Beräknar vi denna summa så får vi

   $$ \frac{5}{30}+\frac{12}{30}=\frac{5+12}{30}=\frac{17}{30}$$

   Nu har vi kommit fram till att summan av 1/6 och 2/5 är lika med 17/30. Detta bråktal kan vi inte skriva i enklare form, så vi är nu klara med uppgiften.

   ---

2. $$\frac{2}{3}-\frac{1}{6}$$
   Vi ser att termerna har olika nämnare (3 och 6), så vi behöver skriva om dem så att de har gemensam nämnare innan vi kan subtrahera dem.

   I just det här fallet behöver vi inte förlänga båda termerna, eftersom vi enkelt kan skriva om den första termen så att den står skriven i sjättedelar. Vi gör detta genom att vi förlänger den första termen med 2:

   $$ \frac{2}{3}=\frac{2\,{\color{Red}{ \cdot \,2}}}{3\,{\color{Red} {\cdot \,2}}}=\frac{4}{6}$$

   Nu är båda termerna skrivna som sjättedelar. Därför kan vi nu subtrahera dem:

   $$ \frac{2}{3}-\frac{1}{6}=\frac{4}{6}-\frac{1}{6}=\frac{4-1}{6}=\frac{3}{6}$$

   3/6 är inte skrivet i sin enklaste form, eftersom både täljaren och nämnaren kan divideras med 3. Därför förkortar vi 3/6 med 3 och får detta:

   $$ \frac{3}{6}=\frac{\,\,\frac{3}{{\color{Red} 3}}\,\,}{\frac{6}{{\color{Red} 3}}}=\frac{1}{2}$$

   Nu har vi alltså kommit fram till att om vi subtraherar 2/3 och 1/6 så får vi 1/2, vilket är svaret skrivet i sin enklaste form.

   (Om vi inte hade sett att vi kunde skriva om 2/3 i sjättedelar, då hade vi kunnat multiplicera nämnarna 3 och 6, och fått den gemensamma nämnaren 18. Det innebär att vi hade kunnat skriva termerna i artondelar, men svaret hade ändå blivit likadant i sin enklaste form, 1/2.)

---

Videolektioner

I den här videon går vi igenom addition och subtraktion av bråk med samma nämnare.

I den här videon går vi igenom addition och subtraktion av bråk med olika nämnare.

Här tittar vi mer på hur man adderar och subtraherar bråktal med hjälp av förlängning/förkortning.