Ekvationslösning
I årskurs 7 började vi bekanta oss med ekvationer och lärde oss att lösa ekvationer, vilket betyder att vi tar reda på vilka värden variablerna ska ha för att ekvationens båda led ska ha samma värde.
I det här avsnittet ska vi lära oss om olika metoder som vi kan använda för att lösa mer komplicerade ekvationer.
Lösningen till en ekvation
Att lösa en ekvation betyder att vi hittar värden på variabler så att ekvationens vänstra led blir lika med ekvationens högra led.
Ett exempel på en ekvation är
$$ x+5=12$$
Den här ekvationens vänstra led är x + 5 och dess högra led är 12. Att lösa den här ekvationen innebär att vi hittar ett värde på variabeln x som gör att x + 5 blir lika med 12.
Ekvationslösning genom balansering
Det finns olika sätt att komma fram till en ekvations lösning. I årskurs 7 löste vi ekvationer av typen
$$ x+5=12$$
genom att fråga oss vilket tal plus 5 som blir lika med 12. Detta tal måste vara lika med 7, så ekvationens lösning är x = 7.
Det här sättet att lösa ekvationer duger bra så länge inte ekvationerna är alltför komplicerade, men i det här avsnittet ska vi lära oss att använda en bättre metod.
Det är nämligen så att vi kan addera, subtrahera, multiplicera eller dividera uttrycken i en ekvation med vilket tal som helst (förutom division med noll, som aldrig är tillåtet), så länge vi gör likadant i ekvationens båda led.
Den här metoden kallas ibland balansering, eftersom den innebär att om vi gör något i det ena ledet, så måste vi göra samma sak i det andra ledet. Så länge vi håller den här balansen kommer de båda sidorna att vara lika stora.
Det kan hjälpa att tänka på balansering som att vi har en gammaldags våg, där innehållet i vågens båda vågskålar ska väga lika mycket för att vågen ska vara i balans. Om vi har en våg och har 4 äpplen i vardera vågskålen, då är vågen i balans.
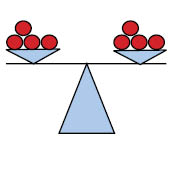
Lägger vi till ett äpple i den vänstra vågskålen, så måste vi också lägga ett äpple i den högra vågskålen för att vågen ska förbli i balans.
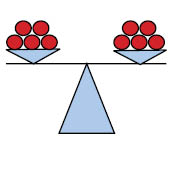
Vad vi vill göra med hjälp av balansering är att genom de fyra räknesätten skriva om ekvationen, så att variabeln står ensam i det ena ledet och det andra ledet innehåller det värde som variabeln måste ha.
Exempel på ekvationslösning med balansering
Vi ska nu visa hur vi löser några olika ekvationer med hjälp av balansering. Först ska vi lösa fyra ekvationer med vart och ett av de fyra räknesätten. Sedan ska vi lösa en mer komplicerad ekvation genom att steg för steg använda två räknesätt efter varandra.
Lös ekvationen
$$ x+5=12$$
Vi vill att variabeln x ska stå ensam i det vänstra ledet. Det kan vi se till att den gör, genom att vi subtraherar 5 från de båda leden. Då får vi det här:
$$x+5=12$$
$$x+5\,{\color{Red} {-\,5}}=12\,{\color{Red} {-\,5}}$$
$$x=7$$
Lös ekvationen
$$ y-3=6$$
För att lösa ekvationen ska variabeln y stå ensam i det ena ledet. Det kan vi få till genom att vi adderar 3 till båda leden i ekvationen:
$$y-3=6$$
$$y-3\,{\color{Blue} {+\,3}}=6\,{\color{Blue}{ +\,3}}$$
$$y=9$$
Lös ekvationen
$$ \frac{x}{6}=3$$
Vi vill att variabeln x ska stå ensam i det ena ledet. Det kan vi uppnå genom att vi multiplicerar båda leden med 6:
$$\frac{x}{6}=3$$
$${\color{Blue} {6\,\cdot}}\, \frac{x}{6}={\color{Blue} {6\,\cdot}}\, 3$$
$$\frac{6x}{6}=18$$
$$x=18$$
Lös ekvationen
$$ 7z=35$$
Vi vill att variabeln z ska stå ensam i det ena ledet. Det kan vi uppnå genom att vi dividerar båda leden med 7:
$$ 7z=35$$
$$\frac{7z}{{\color{Red} {7}}}=\frac{35}{{\color{Red} 7}}$$
$$z=5$$
Lös ekvationen
$$ 4x+5=13$$
Det här är en lite mer komplicerad ekvation, där vi kommer att använda två räknesätt efter varandra för att hitta lösningen.
Vi vill att variabeln x ska stå ensamt i det ena ledet. Eftersom vi har en term 4x i det vänstra ledet, ska vi försöka bli av med termen 5. Det gör vi genom att vi subtraherar 5 från båda leden:
$$4x+5=13$$
$$4x+5\,{\color{Red}{ -\,5}}=13\,{\color{Red} {-\,5}}$$
$$4x=8$$
I det vänstra ledet har vi nu bara en variabelterm, 4x. Men vi vill ju att det bara ska stå x utan en 4:a framför, så vi får lov att dividera båda leden med 4:
$$4x=8$$
$$\frac{4x}{{\color{Blue} 4}}=\frac{8}{{\color{Blue} 4}}$$
$$x=2$$
Nu har vi hittat lösningen till ekvationen: x = 2.
På liknande sätt kan vi lösa mer komplicerade ekvationer steg för steg, vilket är vad vi ska göra i nästa avsnitt.
Videolektioner
Här går vi igenom ekvationslösning i ett steg.
I den här videon går vi igenom ekvationslösning.
