Fyrhörningar
I årskurs 7 började vi lära oss om fyrhörningar och om hur vi beräknar omkrets och area för olika typer av fyrhörningar.
I det här avsnittet ska vi repetera en del av de samband som gäller för olika typer av fyrhörningar. Vi kommer även att undersöka vad vi kan veta om vinkelsummor som gäller för fyrhörningar.
Olika typer av fyrhörningar
En fyrhörning är en geometrisk figur som har fyra hörn, som binds samman av fyra sidor. Hörnen betecknar vi ofta med bokstäver, till exempel A, B, C och D. Vinkelsumman i en fyrhörning är alltid 360°.
Vi ska nu repetera fyra vanligt förekommande fyrhörningar och hur vi beräknar omkrets och area för dessa figurer: rektangel, kvadrat, parallellogram och romb.
Rektangel
En rektangel är en fyrhörning som bara har räta vinklar.
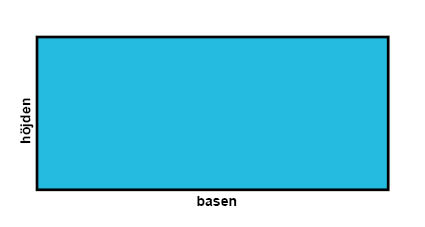
En konsekvens av att rektangeln bara har räta vinklar är att de motstående sidorna i en rektangel är lika långa. När vi ska beräkna en rektangels omkrets eller area brukar vi benämna dessa sidor basen (b) respektive höjden (h).
För rektanglar gäller att omkretsen, O, beräknas enligt denna formel:
$$ O=2b+2h$$
Arean, A, beräknas enligt formeln
$$ A=b\cdot h$$
Låt oss titta på ett exempel
En rektangel har basen 20 cm och höjden 10 cm.
Hitta en annan rektangel som har dubbelt så stor
a) omkrets som den givna rektangeln.
b) area som den givna rektangeln.
Lösningsförslag
a)
Vi ska hitta en rektangel som har dubbelt så stor omkrets som en rektangel med basen 20 cm och höjden 10 cm.
Eftersom omkretsen är lika med summan av sidornas längder, behöver vi bara fördubbla sidornas längder för att också omkretsen ska bli dubbelt så stor.
Omkretsen hos den mindre rektangeln kan vi beräkna så här:
$${O}_{mindre}=2b+2h=$$
$$=2\cdot 20+2\cdot 10=$$
$$=40+20=60\,cm$$
Låter vi såväl basen som höjden i den större rektangeln vara dubbelt så långa som i den mindre, då får vi alltså den här omkretsen:
$${O}_{större}=2\cdot 40+2\cdot 20=$$
$$=80+40=120\,cm$$
En rektangel med basen 40 cm och höjden 20 cm har alltså dubbelt så stor omkrets som rektangeln med basen 20 cm och höjden 10 cm.
b)
Vi ska hitta en rektangel som har dubbelt så stor area som en rektangel med basen 20 cm och höjden 10 cm.
En rektangels area beräknar vi med formeln
$$ A=b\cdot h$$
Den mindre rektangeln har därför arean
$$ {A}_{mindre}=b\cdot h=20\cdot 10=200\,{cm}^{2}$$
Den större rektangeln ska ha dubbelt så stor area, det vill säga
$$ 2\cdot {A}_{mindre}=2\cdot b\cdot h=2\cdot 20\cdot 10=400\,{cm}^{2}$$
Hur kan vi då göra en rektangels area dubbelt så stor? Jo, det kan vi göra till exempel genom att låta rektangelns ena sida vara dubbelt så lång. Det innebär att vi kan låta basen vara 40 cm lång, istället för 20 cm, för att arean ska bli dubbelt så stor, 400 cm².
En rektangel med basen 40 cm och höjden 10 cm har alltså dubbelt så stor area som rektangeln med basen 20 cm och höjden 10 cm.
Kvadrat
En kvadrat har många likheter med en rektangel - i själva verket är en kvadrat en rektangel där alla sidor har samma längd.

Att alla sidorna i en kvadrat har samma längd innebär att det blir enkelt att beräkna en kvadrats omkrets och area. För enkelhets skull skriver vi ofta sidans längd som s.
Omkretsen, O, beräknar vi med formeln
$$ O=4s$$
Arean, A, beräknar vi så här:
$$ A=s\cdot s={s}^{2}$$
(Som vi kom fram till i avsnittet om potenser, är s\(^2\) ett annat sätt att skriva s multiplicerat med sig självt.)
Parallellogram
En parallellogram är en fyrhörning där motstående sidor är lika långa.
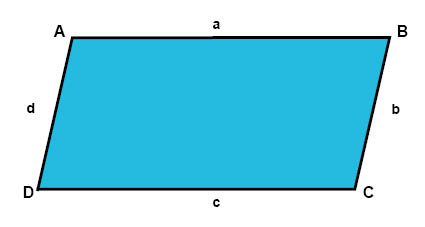
Vinklarna i en parallellogram får vara räta vinklar, men behöver inte vara det.
Om vi utgår från de beteckningar vi använder i figuren här ovanför, kan vi skriva en parallellograms omkrets, O, så här:
$$ O=2a+2b$$
Att finna en parallellograms area kan vara lite knepigt. På samma sätt som vi kom fram till för rektanglar, beräknar vi en parallellograms area genom att multiplicera basen med höjden. Men för parallellogram är basen, b, en av dess sidor och höjden, h, är den vinkelräta sträckan mellan basen och basens motstående sida.

Arean, A, kan vi därför beräkna som
$$ A=b\cdot h$$
Romb
En romb är en parallellogram där fyrhörningens alla sidor har samma längd.

En rombs omkrets, O, blir därför lätt att beräkna, om vi känner till längden på rombens sida, s:
$$ O=4s$$
När vi vill teckna arean för en romb använder vi precis samma formel som för parallellogram. Även i fallet med romber får vi vara noga med att höjden, h, är den vinkelräta sträckan mellan basen och basens motstående sida:
$$ A=b\cdot h$$
Videolektioner
Här går vi igenom olika typer av fyrhörningar.
Här går vi igenom fyrhörningarnas area och omkrets.
I den här videon går vi igenom fyrhörningar.
