Negativa tal
I tidigare årskurser har vi lärt oss om de naturliga talen och decimaltalen.
I det här avsnittet ska vi undersöka tal som är mindre än noll: de negativa talen. Vi börjar med en repetition av hur de naturliga talen och decimaltalen fungerar.
Naturliga tal och decimaltal
När vi vill beskriva hur många eller hur mycket något är, till exempel att det finns 24 elever i klassen eller att en bok har 45 sidor, då använder vi oss vanligtvis av de naturliga talen. De naturliga talen är heltal som är lika med noll eller har positiva värden.
$$ De\,naturliga\,talen:\,0,\,1,\,2,\,3,\,...$$
Vi kan markera de naturliga talen på tallinjen:

Vi har även använt oss av decimaltal, vilka är tal som utöver en heltalsdel även kan innehålla en decimaldel, som består av tiondelar, hundradelar, tusendelar, och så vidare. Tre exempel på decimaltal är talen
$$1,3$$
$$5,47$$
$$0,861476$$
Om du vill repetera hur dessa typer av tal fungerar, så kan du läsa mer i avsnittet om naturliga tal och decimaltal.
Negativa tal
Vi ska nu undersöka de negativa talen, vilka är tal som är mindre än noll. Ett negativt tal skriver vi på samma sätt ett positivt tal, men med ett minustecken, -, framför. Det finns både negativa heltal och negativa decimaltal, men i det här avsnittet ska vi främst titta på de negativa heltalen.
Ett exempel på användning av negativa tal är minusgraderna på en vanlig termometer (som anger temperaturen i grader Celsius). Minusgraderna på termometern är mindre än noll grader (0°C). Till exempel kan vi med hjälp av en termometer läsa av temperaturen -8°C, vilket är 8°C mindre än 0°C.
Negativa tal på tallinjen
På en tallinje är de negativa talen placerade till vänster om noll:
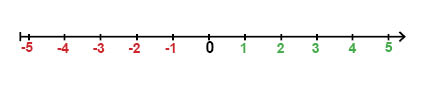
Om vi tittar på tallinjen, kan vi se att avståndet till noll är lika långt från till exempel det negativa talet -1 som från det positiva talet 1, det negativa talet -2 som det positiva talet 2, och så vidare.
När vi använder addition och subtraktion då negativa tal är inblandade, så är det vissa saker som vi bör hålla i minnet. När vi lägger till (adderar) något positivt tal, då rör vi oss åt höger längs tallinjen. När vi drar ifrån (subtraherar) något positivt tal, då rör vi oss åt vänster längs tallinjen.
Har vi att göra med negativa tal, kan det hjälpa att tänka på hur det skulle fungerar på en termometer, när temperaturen ökar eller minskar.
Låt oss titta på ett exempel
$$ -3+4=1$$
Vi kan förstå den här additionen genom att titta på tallinjen. Vi börjar vid det negativa talet -3 och går sedan 4 steg åt höger, eftersom vi adderar ett positivt tal (4). Då hamnar vi vid det positiva talet 1.
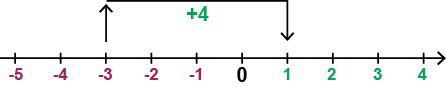
Om vi tänker på hur det fungerar på termometern, så kan vi se det som att vi utgår från temperaturen -3°C och att temperaturen ökar med 4 grader, vilket ger den nya temperaturen +1°C.
På motsvarande sätt kan vi undersöka vad som händer när vi subtraherar ett positivt tal, till exempel
$$ -3-2=-5$$
Om vi tittar på tallinjen, kan vi se den här beräkningen som att vi börjar vid det negativa talet -3 och sedan går 2 steg åt vänster, eftersom vi subtraherar ett positivt tal (2). Då hamnar vi vid det negativa talet -5.
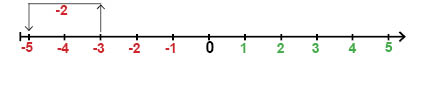
Tänker vi på hur en termometer fungerar, så kan vi se det som att vi går från temperaturen -3°C och temperaturen sedan minskar med 2 grader, vilket ger den nya temperaturen -5°C.
Addera negativa tal
Vi har nu sett vad som händer när vi har ett negativt tal och adderar eller subtraherar positiva tal. Adderar vi ett positivt tal så går vi åt höger längs tallinjen. Subtraherar vi ett positivt tal så går vi åt vänster längs tallinjen.
Men vad händer om vi adderar ett negativt tal? Det ska vi undersöka nu.
Att addera två tal innebär att vi beräknar hur mycket talen är tillsammans. Eftersom negativa tal är mindre än noll, kan vi se dem som en skuld. Om du till exempel har 100 kr på banken och 50 kr i skulder, då har du ju bara 50 kr att köpa för. På samma sätt fungerar det när vi adderar ett negativt tal:
$$ 100+(-50)=100-50=50$$
Att addera -50 är detsamma som att subtrahera 50.
Vi kan tänka så här: om vi har 100 kr och lägger till en skuld på 50 kr, så har vi bara 50 kr kvar. Det är samma sak som om vi hade 100 kr och handlar något (subtraherar) för 50 kr. I båda fallen har vi 50 kr kvar.
På samma sätt kan vi tänka om vi har två negativa tal som vi ska addera. Ska vi till exempel addera talen -100 och -50, får vi det här:
$$ -100+(-50)=-100-50=-150$$
Det kan till exempel vara så att vi har en skuld på 100 kr och ökar skulden med 50 kr. Då blir den sammanlagda skulden 150 kr, alltså har vi -150 kr.
Subtrahera negativa tal
Vi vill också veta vad som händer när vi subtraherar ett negativt tal.
Att subtrahera är att se hur stor skillnaden, differensen, är mellan två tal. Om vi har ett positivt tal och subtraherar ett negativt tal, då kommer skillnaden att bli större än om vi subtraherat ett positivt tal.
Som ett exempel kan vi tänka oss ett flygplan som flyger på höjden 100 meter över vattenytan och en ubåt som befinner sig på djupet 50 meter under vattenytan. Avståndet i höjdled mellan flygplanet och ubåten är 150 meter, eftersom det först är 100 meter från flygplanet till vattenytan och sedan ytterligare 50 meter ner till ubåten. Det här avståndet kan vi se som differensen mellan flygplanets höjd över vattenytan och ubåtens höjd över vattenytan (som är negativ, eftersom ubåten ju är under vattenytan):
$$ 100-(-50)=100+50=150$$
Att subtrahera -50 är detsamma som att addera 50.
Videolektioner
Här går vi igenom negativa tal med hjälp av tallinjen.
Här går vi igenom addition av negativa tal.
Här går vi igenom subtraktion av negativa tal.
I denna video går vi igenom negativa tal på tallinjen.
I den här videon går vi igenom negativa tal i verkligheten.
