Koner

I det här avsnittet ska vi undersöka vad koner är och vi kommer då att märka att de har vissa egenskaper som liknar cylindrar. Även koner kan vi ofta stöta på i vardagen, till exempel i formen av en glasstrut.

Koner

En kon är en geometrisk figur som har en basyta och en mantelyta som formas till en spets utifrån basytan. Om basytan har formen av en cirkel och konens spets ligger rakt ovanför eller under cirkelns medelpunkt, då kallar vi konen för en rak, cirkulär kon. Det är sådana koner som vi vanligtvis menar när vi säger att något föremål har formen av en kon, till exempel en glasstrut.

Så här kan en rak, cirkulär kon se ut:

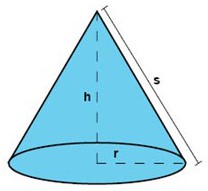
Som vi ser i den här bilden har konen en basyta i form av en cirkel med radien r. Vi ser också att konen har en spets som ligger rak ovanför basytans medelpunkt, på avståndet h.

Volymen av en kon

När vi ska beräkna volymen av en kon kan vi tänka på formeln för en cylinders volym, som vi lärde oss i det förra avsnittet.

En cylinder har volymen

$$ {V}_{cylinder}=B\cdot h$$

Om en kon har samma basyta B och höjd h som en cylinder, så kommer konen att ha en volym som är en tredjedel så stor som cylinderns volym.

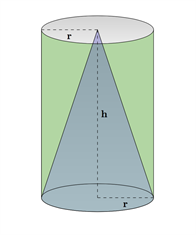
Därför är formeln för en kons volym den här:

$$ {V}_{kon}=\frac{B\cdot h}{3}$$

Om konen har en basyta som har formen av en cirkel med radien r, då kan vi beräkna basytans area så här:

$$ B=\pi{r}^{2}$$

Sätter vi in det här uttrycket i formeln för en kons volym, så får vi för en cirkulär kon den här formeln:

$$ {V}_{kon}=\frac{\pi\cdot {r}^{2}\cdot h}{3}$$

---

Hur stor volym har konen?

En glasstruts insida har formen av en rak, cirkulär kon. Den fylls med glass upp till kanten på struten. Konen har radien 2,5 cm och höjden 10 cm.

Hur stor volym har glassen som struten fyllts med? Svara i milliliter.

Lösningsförslag:

Vi kan använda formeln för en rak, cirkulär kons volym för att beräkna glassens volym, eftersom den helt fyller ut glasstrutens insida.

Konens basyta B är glasstrutens öppning upptill. Den basytan har formen av en cirkel med radien 2,5 cm, så basytans area är

$$ B=\pi\cdot {r}^{2}=\pi\cdot {2,5}^{2}=6,25\pi\,{cm}^{2}\approx 20\,{cm}^{2}$$

Konens höjd h känner vi till och den är 10 cm.

Glasstrutens insidas volym, som också är glassens volym, är därför

$$ {V}_{glasstrut}=\frac{B\cdot h}{3}=\frac{6,25\pi\cdot 10}{3}=\frac{62,5\pi}{3}\approx 65\,{cm}^{3}$$

Med hjälp av formeln för en kons volym kom vi alltså fram till att glassen som struten fylls med har en volym som är ungefär 65 cm³.

Hur mycket är detta i milliliter?

Vi vet sedan avsnittet om volymenheter att 1 kubikcentimeter är lika mycket som 1 milliliter. Därför har glassen en volym som är ungefär 65 ml.

---

Vilken höjd har konen?

En kon har volymen 80 cm³ och en basyta med arean 20 cm².

Lösningsförslag:

I den här uppgiften kan vi använda oss av formeln för en kons volym. Med hjälp av den formeln kan vi lösa ut konens höjd h.

Konens volym är

$$ V=\frac{B\cdot h}{3}$$

I den här formeln vet vi vilka värden V och B ska ha. V är ju konens volym, som vi vet är 80 cm³. B är konens basytas area, som är 20 cm². Det enda i formeln som vi inte vet värdet på är konens höjd h.

Fyller vi i vad vi vet i den här formeln, så får vi den här ekvationen:

$$ 80=\frac{20\cdot h}{3}$$

Den här ekvationen kan vi lösa med hjälp av balansering, som vi lärt oss i tidigare avsnitt. Att lösa ekvationen innebär att vi hittar vilket värde som höjden h måste ha:

$$80=\frac{20\cdot h}{3}$$

$${\color{Blue} 3\,\cdot\,} 80={\color{Blue} 3\,\cdot\,}\frac{20\cdot h}{3} $$

$$240=20\cdot h$$

$$\frac{240}{{\color{Red}{20}}}=\frac{20\cdot h}{{\color{Red}{20}}}$$

$$h=12\,cm$$

Nu har vi alltså kommit fram till att en kon som har volymen 80 cm³ och en basyta med arean 20 cm² måste ha höjden 12 cm.

Videolektion

Här går vi igenom volym för en kon.

Här går vi igenom koner, vad det är och hur man beräknar volymen av en kon.