Negativa tal

I det här avsnittet ska vi repetera hur negativa tal fungerar, och hur vi adderar och subtraherar dessa tal, för att sedan i nästa avsnitt lära oss om hur vi kan multiplicera och dividera negativa tal.

Negativa tal och tallinjen

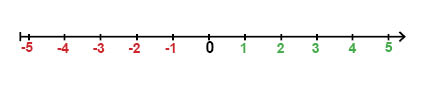
De negativa talen är de tal vars värde är mindre än noll.

Den punkt på tallinjen som markerar talet noll brukar kallas origo. De tal som ligger till höger om origo på tallinjen är de positiva talen, medan de tal som ligger till vänster om origo är de negativa talen.

Addition och subtraktion med negativa tal

När vi ska addera eller subtrahera med negativa tal finns det vissa räkneregler som vi behöver komma ihåg.

Om vi adderar ett negativt tal, är det samma sak som att vi hade subtraherat motsvarande positiva tal.

Ett exempel på detta ser vi här:

$$ 4+(-3)=4-3=1$$

Om vi subtraherar ett negativt tal, är det samma sak som att vi hade adderat motsvarande positiva tal.

Exempelvis gäller:

$$ 4-(-3)=4+3=7$$

Som vi ser är det viktigt att hålla ordning på vilka tecken som används.

En minnesregel för det här är att lika tecken ger plus, medan olika tecken ger minus:

$$ \\4\,{\color{Blue} +}\,({\color{Red} -}3)=4\,{\color{Red} -}\,3=1 $$

$$ 4\,{\color{Red} -}\,({\color{Red} -}3)=4\,{\color{Blue} +}\,3=7$$

Två minustecken ger alltså ett plus:

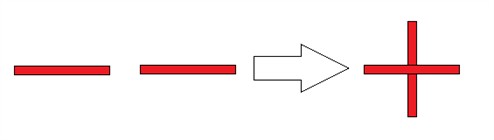
Om talen a och b är positiva tal, då kan vi sammanfatta dessa räkneregler så här:

$$ a+(-b)=a-b $$

$$ a-(-b)=a+b$$

---

Beräkna

$$ a)\,\,1-(-2)+(-3) $$

$$ b)\,\,(-1)+2-(-3)$$

Lösningsförslag:

a) Vi använder räknereglerna steg för steg:

$$1-(-2)+(-3)=$$

$$=1+2+(-3)=$$

$$=1+2-3=$$

$$=3-3=$$

$$=0$$

b) Vi använder räknereglerna steg för steg:

$$(-1)+2-(-3)=$$

$$=-1+2+3=$$

$$=1+3=$$

$$=4$$

Videolektioner

Här går vi igenom negativa tal, vad de är och hur de kan representeras med hjälp av en tallinje.

 

Här går vi igenom addition och subtraktion med negativa tal och använder oss av en metod som tar hjälp av tallinjen.