Funktioner

I det här avsnittet ska vi lära oss om funktioner. Funktioner är samband eller regler som säger oss att om en variabel har ett visst värde, då vet vi vilket värde en annan variabel har. Funktioner används väldigt ofta inom matematiken för att beskriva olika situationer, så därför är det viktigt att vi förstår hur de fungerar.

Vad är en funktion?

Det finns många situationer där vi kan säga att värdet på en viss variabel bestämmer värdet på en annan variabel.

Till exempel är det totala pris som du får betala för äpplen som säljs i lösvikt till priset 15 kr/kg, beroende av den sammanlagda vikten på de äpplen du köper. Vi kan beteckna äpplenas vikt med x och priset vi får betala i kassan med y.

Vi säger då att det pris y vi får betala för äpplena är en funktion av äpplenas vikt x.

Det här sambandet kan vi även skriva så här:

$$ y=15x$$

Allmänt gäller att en funktion är ett samband eller regel som innebär att en viss variabels värde beror på en eller flera andra variablers värden. I vårt exempel gäller alltså att värdet på variabeln y beror på värdet på variabeln x och vi vet i det här fallet att värdet på y blir 15 gånger större än värdet på x.

Vi kan se en funktion som en maskin, där du stoppar in ett visst värde på en variabel i den ena änden och att du då får ut ett visst värde på en annan variabel i maskinens andra ände. Hur själva funktionen ser ut avgör vad "maskinen" gör med det variabelvärde som den tar emot.

Här nedanför ser du en funktion som anger att värdet på variabeln y beror på värdet på variabeln x enligt regeln

$$ y=x+2$$

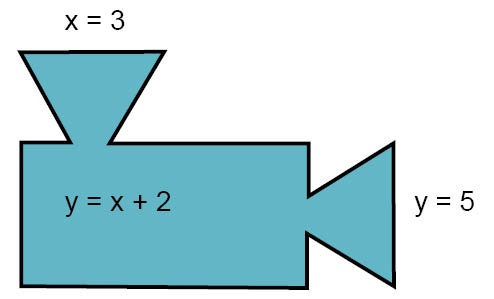
Den här funktionen (regeln) säg oss att y-värdet kommer att vara 2 mer än x-värdet.

Stoppar vi till exempel in variabelvärdet x = 3 i funktionen, så byter vi ut x mot 3 i funktionsuttrycket och då blir värdet på variabeln y detta:

$$y=x+2=$$

$$=3+2=$$

$$=5$$

För att det ska bli extra tydligt att det är en funktion det rör sig om, brukar man skriva att värdet på en variabel y beror på värdet på en variabel x, så här:

$$ y(x)$$

Utifrån vårt exempel med "funktionsmaskinen" ovan, kan vi skriva funktionen så här:

$$ y(x)=x+2$$

Vill vi räkna ut vilket värde variabeln y har när variabeln x har värdet 3, då skriver vi så här:

$$ y(3)=3+2=5$$

En viktig egenskap som funktioner har, är att varje värde som vi stoppar in i en viss funktion alltid ger samma värde ut. Det gör att funktioner är förutsägbara. Ett samband som inte har den här egenskapen kan inte vara en funktion.

Exempel på funktioner

Funktioner förekommer i många olika sammanhang. Här är några exempel på funktioner.

Hur mycket lön Anna har tjänat på sitt extrajobb där hon har timlön är en funktion av hur många timmar hon har arbetat.

Hur lång en cirkels omkrets är kan ses som en funktion av cirkelns radie.

Hur mycket äpplena kostar när de har ett visst kilopris är en funktion av hur mycket de väger.

Hur högt över marken som en kanonkula befinner sig är en funktion av tiden som gått sedan kanonen avfyrades.

Räkna med funktioner

Vi ska nu räkna med några olika funktioner.

---

Annas timlön

Anna arbetar extra och har då en timlön på 80 kr/timme.

Hur mycket lön Anna har tjänat kan vi beteckna med y kr och det antal timmar hon har arbetat kan vi beteckna med x timmar.

Annas intjänade lön y kr kan vi se som en funktion av antalet timmar x hon har arbetat, enligt denna funktion:

$$ y(x)=80x\,kr$$

Beräkna y(10) och tolka vad det uttrycket betyder.

Lösningsförslag:

Vi ska beräkna y(10), så vi sätter in 10 istället för x i funktionen:

$$ y(10)=80\cdot 10\,kr=800\,kr$$

Vi tolkar detta som att Anna har arbetat 10 timmar och för den tiden har hon tjänat 800 kr i lön.

---

En kanonkula skjuts ut ur en kanon

Med variabeln y betecknar vi hur högt över marken (i meter) som kanonkulan befinner sig. Med variabeln t betecknar vi hur lång tid (i sekunder) som gått sedan kanonen avfyrades.

Hur högt över marken som kanonkulan befinner sig kan vi beräkna med hjälp av den här funktionen:

$$ y(t)=-0,7{t}^{2}+5t+1$$

Beräkna y(2) och tolka vad det uttrycket betyder.

Lösningsförslag:

I det här exemplet hade vi ett mer komplicerat funktionsuttryck än i det förra exemplet, men vi räknar på samma sätt.

Vi ska beräkna y(2), så vi sätter in 2 istället för t i funktionen:

$$y(2)=-0,7\cdot {2}^{2}+5\cdot 2+1= $$

$$=-0,7\cdot 4+5\cdot 2+1=$$

$$=-2,8+10+1=$$

$$=8,2$$

Vad är det vi nu har räknat ut?

Jo, y(2) betyder att vi beräknar hur högt över marken som kanonkulan befinner sig 2 sekunder efter det att kanonen har avfyrats.

Vi kom fram till att

$$ y(2)=8,2$$

så det tolkar vi som att kanonkulan efter 2 sekunder befinner sig på höjden 8,2 meter över marken.

På samma sätt kan vi beräkna hur högt över marken som kanonkulan befinner sig vid andra tidpunkter. Allt vi behöver göra är att sätta in en viss tid i sekunder räknat i funktionen, så får vi ut kanonkulans höjd över marken vid just den tidpunkten.

Videolektioner

Här går vi igenom funktioner.

Här fortsätter vi gå igenom funktioner och tar hjälp av funktionsmaskiner.

Här går vi igenom funktioner, vad det är och hur man kan beräkna dem.

Här går vi igenom hur man räknar med funktioner.