Fyrhörningar
I ett tidigare avsnitt har vi lärt oss om vinklar och bland annat stött på räta vinklar.
I det här avsnittet ska vi undersöka olika typer av fyrhörningar, och hur vi kan beräkna dessa fyrhörningars omkrets och area. Vi kommer att se att vi nu kan få användning för vad vi lärt oss om vinklar, för att bättre förstå olika typer av fyrhörningar.
Vad är en fyrhörning?
En fyrhörning är en geometrisk figur som har fyra hörn, som binds samman av fyra sidor. Hörnen betecknar vi ofta med bokstäver, till exempel A, B, C och D.
Sidorna i en fyrhörning betecknar vi ofta med hjälp av de hörn som sidan binder samman. Till exempel kan vi kalla en sida AB om den binder samman hörnen A och B, som i bilden här nedanför. På samma sätt kan vi till exempel kalla en sida BC, om den binder samman hörnen B och C.
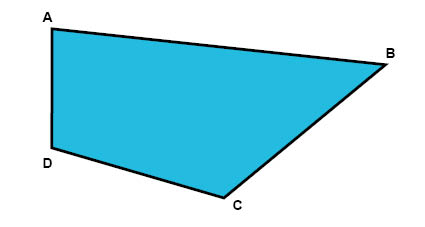
De sidor i en fyrhörning som inte har några gemensamma hörn, kallar vi motstående sidor. I fyrhörningen som vi ser här ovanför gäller därför att sidorna AB och CD är motstående sidor, och att sidorna BC och AD även de är motstående sidor.
De vinklar i en fyrhörning som inte har några gemensamma sidor (vinkelben), kallar vi motstående vinklar. I figuren ovan är vinklarna i hörnen A och C motstående vinklar, och på samma sätt är vinklarna i hörnan B och D motstående.
En diagonal är en linje som binder samman två motstående hörn. I bilden här nedanför har vi ritat in två diagonaler: en diagonal AC, som binder samman hörnen A och C, och en diagonal BD, som binder samman hörnen B och D.
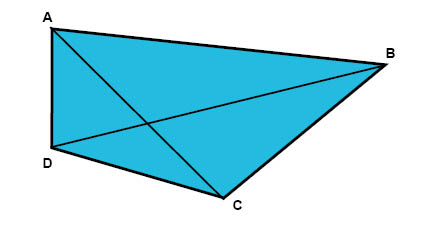
Omkrets och area
Med omkrets menar vi längden av sträckan runt en geometrisk figur, till exempel en fyrhörning. En fyrhörnings omkrets är därför lika med summan av längderna av fyrhörningens sidor. Omkrets betecknas ofta med bokstaven O och anges i längdenheter, till exempel meter (m), centimeter (cm) eller kilometer (km).
En geometrisk figurs area är hur stor yta om ryms i figuren. Har vi till exempel en fyrhörning, så blir det ett visst område som begränsas av fyrhörningens sidor. Arean betecknas ofta med bokstaven A och anges i areaenheter, till exempel kvadratmeter (m2), kvadratcentimeter (cm2) eller kvadratkilometer (km2).
När vi anger ett områdes area som till exempel 1 m2, då menar vi att ytan är lika stor om en kvadrat vars sidor är 1 meter. På samma sätt motsvarar 1 cm2 ytan hos en kvadrat vars sidor är 1 cm.
Olika typer av fyrhörningar
Vi ska nu undersöka några olika typer av fyrhörningar som vi kan träffa på: rektangel, kvadrat, parallellogram och romb. Vi kommer att lära oss hur vi beräknar omkrets och area för var och en av dessa fyrhörningar.
Rektangel
En rektangel är en fyrhörning som bara har räta vinklar, det vill säga att var och en av de fyra vinklarna i fyrhörningen är 90°.
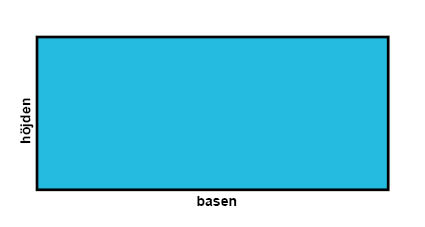
Att rektangelns vinklar är räta innebär att de motstående sidorna i en rektangel är lika långa. När vi ska beräkna en rektangels omkrets och area, då brukar vi kalla sidorna bas och höjd.
En rektangels omkrets är lika med summan av dess sidors längder. Därför kan vi beräkna rektangelns omkrets så här:
$$Omkrets=basen+basen+höjden+höjden=$$
$$=2\cdot basen+2\cdot höjden$$
Ofta betecknar vi basen med b och höjden med h. Därför kan vi skriva omkretsen, O, så här:
$$ O=2b+2h$$
När vi ska beräkna en rektangels area använder vi oss också av basen och höjden.
$$ Area=basen\cdot höjden$$
Om vi använder beteckningarna A för area, och b (basen) och h (höjden), kan vi skriva rektangelns area så här:
$$ A=b\cdot h$$
Beräkna omkrets och area för en rektangel där basen är 6 meter och höjden är 2 meter
Eftersom vi vet att basen är 6 meter och höjden är 2 meter, kan vi skriva det så här:
$$b=6\,m $$
$$h=2\,m$$
Formeln för en rektangels omkrets är
$$ O=2b+2h$$
Därför kan vi beräkna omkretsen som
$$ O=2\cdot 6+2\cdot 2=12+4=16\,m$$
Formeln för en rektangels area är
$$ A=b\cdot h$$
Därför kan vi beräkna arean som
$$ A=6\cdot 2=12\,{m}^{2}$$
Rektangelns omkrets är alltså 16 meter och dess area är 12 m².
Kvadrat
En kvadrat är en rektangel där alla sidorna har samma längd.
Det innebär att det blir enklare att räkna ut en kvadrats omkrets och area. Eftersom sidorna är lika långa, brukar vi helt enkelt kalla dem kvadratens sida, vilket vi kan beteckna med bokstaven s.

En kvadrats omkrets är lika med summan av sidornas längder, vilket blir:
$$ Omkrets=sidan+sidan+sidan+sidan=4\cdot sidan$$
Om vi använder beteckningen O för kvadratens omkrets och s för längden av kvadratens sida, så kan vi skriva omkretsen så här:
$$ O=4s$$
När vi ska beräkna en kvadrats area utgår vi från formeln för en rektangels area. Eftersom kvadratens sidor alla är lika långa, får vi den här formeln för kvadratens area:
$$ Area=sidan\cdot sidan$$
Med beteckningen A för area och s för sidans längd, får vi
$$ A=s\cdot s$$
Parallellogram
En parallellogram är en fyrhörning där motstående sidor är lika långa.
Till skillnad från rektanglar och kvadrater finns det inte något krav på att en parallellograms vinklar ska vara räta. En parallellograms vinklar kan vara räta, men behöver inte vara det.
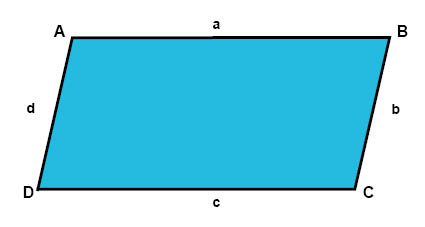
För parallellogram gäller att motstående sidor är lika långa. I figuren ovan gäller alltså det här:
$$a=c$$
$$b=d$$
Eftersom vi vet att motstående sidor är lika långa, kan vi skriva parallellograms omkrets, O, så här:
$$ O=2a+2b$$
där sidorna a och b motsvarar dem i figuren ovan.
Att finna en parallellograms area är lite knepigt. På samma sätt som vi kom fram till för rektanglar, beräknar vi en parallellograms area genom att multiplicera basen och höjden. Men för parallellogram är basen, b, en av dess sidor och höjden, h, är den vinkelräta sträckan mellan basen och basens motstående sida.

Vi beräknar därför parallellogrammens area så här:
$$ A=b\cdot h$$
Romb
En romb är en parallellogram där fyrhörningens alla sidor har samma längd.

Rombens omkrets, O, blir därför lätt att beräkna, om vi känner till längden på rombens sida, s:
$$ O=4s$$
När vi vill teckna arean för en romb använder vi precis samma formel som för parallellogram:
$$ A=b\cdot h$$
där basen b är en av rombens sidor och höjden h är den vinkelräta sträckan mellan basen och basens motstående sida.
Videolektioner
I den här videon går vi igenom fyrhörningar genom att titta på olika typer av fyrhörningar.
I den här videon går vi igenom omkrets och area på fyrhörningar.
I den här videon går vi igenom några viktiga begrepp för att beskriva en fyrhörning.
I den här videon går vi igenom hur vi beräknar omkrets och area på en fyrhörning.
