Multiplikation med decimaltal
Tidigare har vi gått igenom de fyra räknesätten, bland annat multiplikation och division. I föregående avsnitt har vi även tittat närmare på hur vi gör när vi multiplicerar med 10, 100 och 1000 eller dividerar med 10, 100 och 1000.
I det här avsnittet ska vi använda det vi lärt oss i tidigare avsnitt, när vi nu undersöker hur vi kan multiplicera decimaltal.
Multiplikation med decimaltal
Vi har tidigare träffat på hur vi gör då vi multiplicerar heltal med varandra. Till exempel kan vi då använda oss av multiplikationstabellen.
Hur går det till om vi vill multiplicera med decimaltal? Till exempel kan vi vilja beräkna den här produkten:
$$ 20\cdot 0,3$$
När vi ska beräkna denna produkt kan det hjälpa att skriva om decimaltalet 0,3 så här:
$$ 0,3=3\cdot 0,1$$
Uttrycket i sin helhet blir då
$$ 20\cdot 3\cdot 0,1$$
Denna produkt bör vi kunna beräkna, eftersom vi sedan tidigare vet hur vi multiplicerar med en tiondel (0,1). Vi får
$$ 20\cdot 3\cdot 0,1=60\cdot 0,1=6$$
På motsvarande sätt kan vi lättare beräkna många uttryck som innehåller decimaltal.
Beräkna
$$15\cdot 0,6$$
Vi börjar med att skriva om decimaltalet 0,6 så här:
$$ 0,6=6\cdot 0,1$$
När vi har kommit så här långt kan vi lättare beräkna den ursprungliga produkten. Vi får
$$15\cdot 0,6=$$
$$=15\cdot 6\cdot 0,1=$$
$$=90\cdot 0,1=9$$
Svar: 9
Beräkna
$$0,2\cdot 0,7$$
Även i den här uppgiften kan vi skriva om decimaltalen, så här:
$$ 0,2=2\cdot 0,1$$
$$och$$
$$ 0,7=7\cdot 0,1$$
Sammantaget kan vi nu lätt beräkna den ursprungliga produkten, om vi gör det steg för steg. Vi får
$$0,2\cdot 0,7=$$
$$=2\cdot 0,1\cdot 7\cdot 0,1=$$
$$=14\cdot 0,1\cdot 0,1=$$
$$=14\cdot 0,01=0,14$$
Svar: 0,14
Uppställning av multiplikation med decimaltal
Hur gör vi när vi ska multiplicera decimaltal som är större än 1, alltså de tal som inte har en nolla framför kommatecknet? Ett bra sätt är med uppställning och det är oftast lättare när man har tal som innehåller många siffror.
Vi visar med exemplet 5,2 \(\cdot\) 1,4:
Vi sätter faktorn som är högst överst i uträkningen:
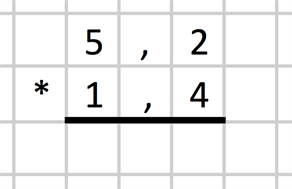
Vi börjar med att multiplicera tiondelen i faktorn vi la underst i uträkningen, alltså siffran 4, med tiondelen i den översta faktorn, alltså siffran 2. Det är 8, som vi sätter längst till höger under strecket:
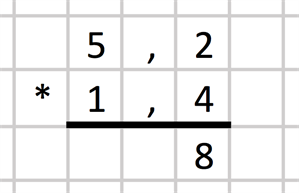
Vi fortsätter att multiplicera tionedelen 4 men nu med entalet 5 i faktorn ovan. Det är 20, som vi placerar till vänster om 8:an under strecket:
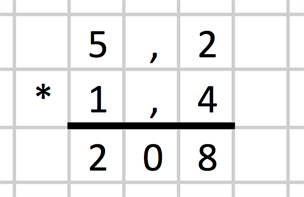
Nu har vi multiplicerat siffran längst till höger i den undre faktorn med alla tal i den översta faktorn. Nästa steg är att ta talet till vänster om 4:an och multiplicera det talet med alla tal i faktorn ovan. Det är entalet 1, och vi börjar att multiplicera det med tionedelen 2, vilket är 2. Denna två hamnar under nollan. Här är det viktigt att komma ihåg att hoppa ett steg åt vänster i uträkningen:
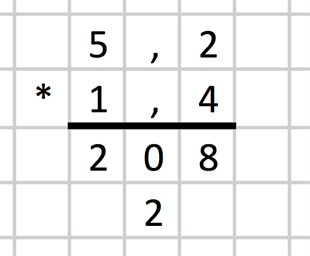
Nu multiplicerar vi entalet 1 med entalet 5, vilket är 5. Denna siffra placerar vi till vänster om tvåan:
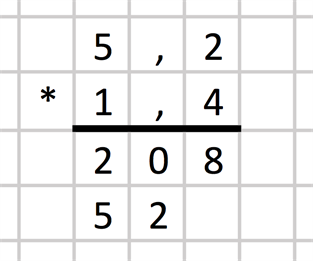
Alla tal är nu multiplicerade med varandra, nästa steg är att addera ihop de två rader vi fick fram i uträkningen, med hjälp av additionsuppställning:

Sista steget är att placera ut kommatecknet. Eftersom vi har två faktorer som båda har en tiondel kommer vår produkt att innehålla en tiondel och en hundradel. Kommatecknet ska alltså ha två siffror till höger om sig och svaret blir därför 7,28. Man kan tänka att så många decimaltal som faktorerna har gemensamt, så många decimaltal ska produkten ha.
Svar: 7,28
Videolektioner
I den här videon går vi igenom multiplikation med decimaltal.
Här visar vi hur man multiplicerar decimaltal med hjälp av en enkel metod.
