Trianglar
I årskurs 7 lärde vi oss om olika typer av trianglar, och hur vi beräknar omkrets och area för en triangel. Vi har även tidigare studerat vinklar, så vi vet nu bland annat vad en vinkelsumma är.
I det här avsnittet ska vi repetera trianglars vinkelsummor, några olika typer av trianglar, och trianglars omkrets och area.
Trianglars egenskaper
En triangel är en geometrisk figur som har tre hörn. I vart och ett av triangelns hörn finns en vinkel och hörnen är sammanbundna av tre sidor.
Trianglar har alltid en vinkelsumma som är lika med 180°. Denna vinkelsumma får vi genom att vi adderar triangelns tre vinklar.
Har vi vill exempel en triangel med vinklarna 25°, 65° och 90°, så blir vinkelsumman
$$ {25}^{\circ}+{65}^{\circ}+{90}^{\circ}={180}^{\circ}$$
Att vinkelsumman i en triangel alltid måste vara just 180° är en egenskap som vi kan använda. Vet vi till exempel storleken på två av triangelns vinklar, så kan vi enkelt beräkna storleken på den tredje vinkeln.
Triangelns vinklar
I figuren här nedanför är två av vinklarna i en triangel 60° respektive 70°.
Kan den tredje vinkeln v i triangeln ha storleken 40°?
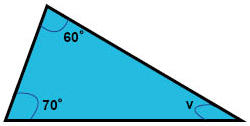
Lösningsförslag:
Vi vet att en triangels vinkelsumma alltid ska vara lika med 180°. Därför kan vi teckna en ekvation för vinkelsumman, som ser ut så här:
$$ {60}^{\circ}+{70}^{\circ}+v={180}^{\circ}$$
Den här ekvationen löser vi:
$${60}^{\circ}+{70}^{\circ}+v={180}^{\circ}$$
$${130}^{\circ}+v={180}^{\circ} $$
$${130}^{\circ}+v\,{\color{Red} -\,{130}^{\circ}}={180}^{\circ}\,{\color{Red} -\,{130}^{\circ}} $$
$$v={50}^{\circ}$$
Vi kom alltså fram till att vinkeln v måste vara 50°, så den kan inte vara 40°.
Olika typer av trianglar
Vi känner nu till att en triangels vinkelsumma alltid måste vara lika med 180°. Det finns tre speciella typer av trianglar som förekommer ofta, som vi bör känna till, eftersom de har användbara samband mellan sina vinklar och sidor.
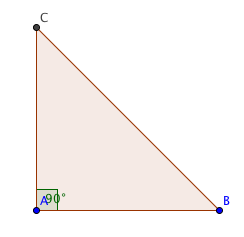
Rätvinkliga trianglar
En rätvinklig triangel är en triangel som har en rät vinkel, det vill säga en vinkel som är 90°. Att en vinkel i en triangel är rät innebär också att de två övriga vinklarna tillsammans är 90°, eftersom vinkelsumman i en triangel alltid är 180°.
Likbenta trianglar
En likbent triangel är en triangel där två sidor är lika långa.
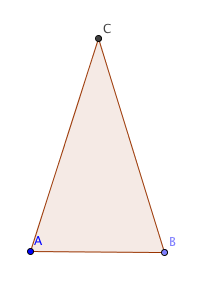
Eftersom de båda sidorna AC och BC i triangeln ovan är lika långa är triangeln likbent.
En användbar egenskap hos likbenta trianglar är att två av triangelns vinklar är lika stora. I figuren ovan är det vinklarna vid hörnen A och B som är lika stora. De vinklar i en likbent triangel som har denna egenskap kallar vi basvinklar.
Liksidiga trianglar
En liksidig triangel är en triangel där alla sidorna är lika långa.
En annan användbar egenskap hos liksidiga trianglar är att triangelns tre vinklar alla är lika stora. Eftersom vinkelsumman i en triangel är 180°, måste var och en av den liksidiga triangelns vinklar vara 60°:
$$ 3v={180}^{\circ} $$
$$v=\frac{{180}^{\circ}}{3}={60}^{\circ}$$
Trianglars omkrets och area
En triangels omkrets, O, är lika med summan av sidornas längd. För en allmän triangel med sidor a, b och c, kan vi skriva omkretsen så här:
$$ O=a+b+c$$
När vi ska komma fram till en formel för trianglars area, kan det vara bra att tänka på en triangel som hälften av en parallellogram.
I figuren här nedanför har vi skissat in en parallellogram, vars area alltså är dubbelt så stor som triangeln i samma figur.

Som vi vet från avsnittet om fyrhörningar, kan vi beräkna en parallellograms area som basen multiplicerat med höjden. Eftersom triangelns area är hälften så stor som en parallellogram med samma bas och höjd, skriver vi triangelns area så här:
$$ {A}=\frac{b\cdot h}{2}$$
Beräkna denna triangels omkrets och area
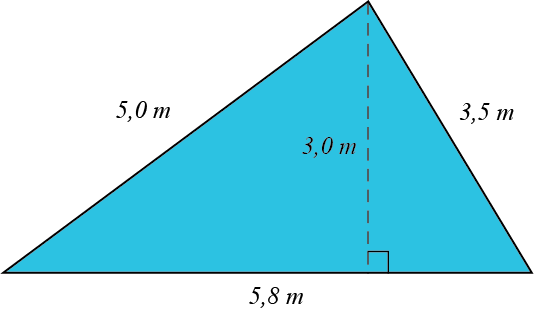
Lösningsförslag:
Omkretsen är lika med summan av sidornas längd, vilka vi läser av i figuren:
$$ O=3,5+5,0+5,8=14,3\,m$$
Triangelns omkrets är alltså 14,3 meter.
När vi ska beräkna triangelns area börjar vi med att identifiera basen och höjden. Ur figuren ser vi att basens längd är lika med 5,8 meter och höjdens längd är lika med 3,0 meter. Därför kan vi beräkna triangelns area så här:
$$ A=\frac{b\cdot h}{2}=\frac{5,8\cdot 3,0}{2}=\frac{17,4}{2}=8,7\,{m}^{2}$$
Triangelns area är alltså 8,7 m2.
Videolektioner
Här går vi igenom trianglar.
Här går vi igenom trianglars area och omkrets.
I den här videon går vi igenom trianglar.
