Rätblock och kuber

I det här avsnittet ska vi lära oss mer om kuber och rätblock. Vi kommer också att märka att kuber i själva verket är en typ av rätblock.

Rätblock och kuber

En kub är en tredimensionell figur som har längd, bredd och höjd som är lika långa. Alla vinklar hos kuben är räta vinklar.

Exempel på kubformade föremål som du kan ha träffat på redan är en vanlig sexsidig tärning eller en låda som har sex stycken kvadratformade sidor.

Ett rätblock är en tredimensionell figur som precis som kuber har en längd, bredd och höjd, och vinklar som alla är räta vinklar. Men ett rätblocks längd, bredd och höjd behöver inte vara lika långa.

Exempel på rätblocksformade föremål är en tegelsten eller en vanlig skokartong.

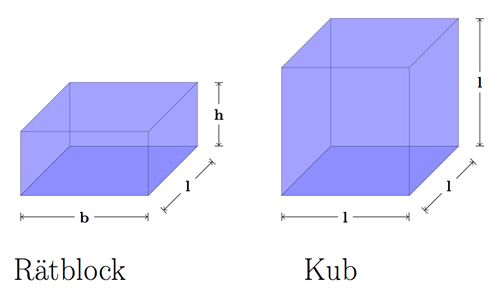
Alla kuber är även rätblock - en kub är helt enkelt ett rätblock där sidornas längd är lika långa. Däremot är inte alla rätblock kuber.

Volymen av ett rätblock eller kub

När vi vill räkna ut hur stor volym som ett rätblock har, börjar vi med att titta på vilka kanter som är rätblockets längd (l) och bredd (b). Längden och bredden skapar tillsammans en yta, basytan, som har formen av en rektangel, vars area vi kallar basarean. Den här basarean multiplicerar vi sedan med rätblockets höjd (h), för att få rätblockets volym.

Om rätblocket i den förra figuren här ovanför har längden 4 cm, bredden 4 cm och höjden 2 cm, så kan vi beräkna volymen. Först räknar vi ut hur stor basarean är. Sedan multiplicerar vi basarean med höjden, för att få volymen.

Vi vet från årskurs 8 hur vi beräknar arean av en rektangel.  På samma sätt kan vi beräkna hur stor basarean (B) är:

$$ Basarea=längd\cdot bredd$$

$$B=l\cdot b$$

Om rätblocket har längden 4 cm och bredden 4 cm, då blir alltså basarean 16 cm\(^2\):

$$ B=4\,cm\cdot 4\,cm=16\,{cm}^{2}$$

För att få volymen multiplicerar vi basarean med höjden:

$$ Volym=basarea\cdot höjd $$

$${V}_{rätblock}=B\cdot h$$

Om rätblockets basarea är 16 cm\(^2\) och höjden är 2 cm, då blir alltså rätblockets volym 32 cm\(^3\):

$$ {V}_{rätblock}=B\cdot h=16\,{cm}^{2}\cdot 2\,cm=32\,{cm}^{3}$$

Om vi vill så kan vi även skriva ett rätblocks volym så här:

$$Volym=längd\cdot bredd\cdot höjd$$

$${V}_{rätblock}=l\cdot b\cdot h$$

En kub är helt enkelt ett rätblock där sidornas längd är lika långa. Därför kan vi skriva en kubs volym ännu enklare. Vi betecknar sidornas längd med l och kan då skriva volymen så här:

$$Volym=längd\cdot längd\cdot längd$$

$${V}_{kub}=l\cdot l\cdot l={l}^{3}$$

---

Beräkna högtalarens volym

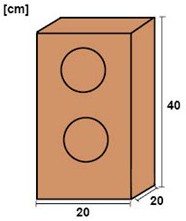
En högtalare ser ut som i den här bilden. Ange volymen dels i enheten cm³ och dels i enheten liter.

Lösningsförslag:

Som vi ser i bilden har högtalaren formen av ett rätblock. Rätblocket har längden 20 cm, bredden 20 cm och höjden 40 cm.

Vi kan beräkna högtalarens volym med hjälp av formeln för ett rätblocks volym, så här:

$$ {V}_{högtalare}=l\cdot b\cdot h=20\,cm\cdot 20\,cm\cdot 40\,cm=16\,000\,{cm}^{3}$$

Det går lika bra att först beräkna basarean B och sedan använda den och höjden h för att beräkna volymen, vilket vi kan göra så här:

$$ B=l\cdot b=20\,cm\cdot 20\,cm=400\,{cm}^{2}$$

När vi nu har basarean B, beräknar vi volymen:

$$ {V}_{högtalare}=B\cdot h=400\,{cm}^{2}\cdot 40\,cm=16\,000\,{cm}^{3}$$

Volymen blir alltså likadan oavsett vilket av dessa sätt vi använder.

Nu har vi beräknat volymen i enheten cm\(^3\), men vi vill ju även ta reda på hur mycket den här volymen är räknat i liter. Från avsnittet om volym och volymenheter vet vi att

$$ 1\,{cm}^{3}=0,001\,l$$

Därför kan vi skriva om volymen till enheten liter, så här:

$$ 16\,000\,{cm}^{3}=16\,000\cdot 0,001\,l=16\,l$$

Högtalarens volym är alltså 16 000 cm\(^3\), vilket är samma sak som 16 liter.

Videolektioner

Här går vi igenom volym för en kub.

Här går vi igenom volym för ett rätblock.

Här går vi igenom rätblock och kuber, samt hur vi beräknar volymen av dessa två figurer.