Linjär optimering

Linjär optimering handlar om att optimera en fuktion \(z\). Denna funktion är en linjär funktion i flera variabler. Allmänt skriver vi funktionen som

$$z=\sum_{k=1}^nc_kx_k$$

Det generella linjära optimeringsproblemet går ut på att minimera ovan nämnda funktion, under bivillkoren:

$$\begin{align}\begin{cases}a_{1,1}x_1+a_{1,2}x_2+\dots+a_{1,n}x_n\leq b_1\\a_{2,1}x_1+a_{2,2}x_2+\dots+a_{2,n}x_n\leq b_2\\ \vdots\\a_{m,1}x_1+a_{m,2}x_2+\dots+a_{m,n}x_n\leq b_m\end{cases}\end{align}$$

Alla \(x_k\) står för de olika beslut som kan tas och konstanterna \(c_k\) är kostnaderna för varje beslut. Bivillkoren går att skriva mycket mer kompakt med hjälp av matriser. 

Låt A vara matrisen bestående av elementen \(a_{i,j}\), \(x\) får representera kolumnvektorn med elementen \(x_1,\dots,x_n\) och \(b\) är kolumnvektorn med elementen \(b_1,\dots,b_n\). Då kan vi skriva om bivillkoren som

$$Ax\leq b$$

Bivillkoren utformar ett område i \(n\) dimensioner. Generellt kan detta sammanfattas som:

$$\begin{align}\begin{cases}\min \sum_{k=1}^nc_kx_k\\ \text{s.a. }Ax\leq B\end{cases}\end{align}$$

där s.a. står för "sådant att".

Linjär optimering i två dimensioner

För att underlätta kommer vi från och med nu hålla oss till två dimensioner. Detta gör att funktionen \(z\) kan skrivas på följande sätt:

$$z=ax+by$$

där a och b är konstanter och x och y är våra obekanta variabler.

I två dimensioner kan bivillkoren representeras av en sluten yta. Till exempel kan bivillkoren leda till följande yta:

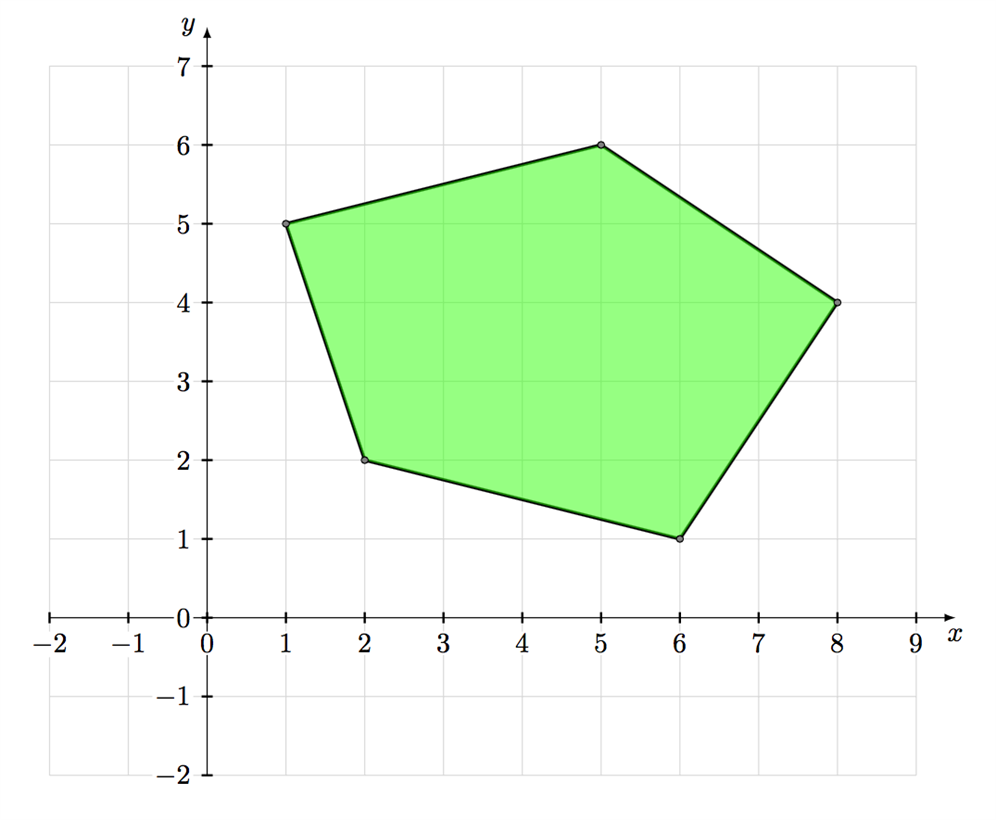
Vår uppgift är således att optimera funktionen 

$$z=ax+by$$

inom detta område. Idén är att vi sätter z till något fixt värde, säg C, och skriver om funktionen till en linjär funktion:

$$\begin{align}C&=ax+by\\&\iff\\y&=\frac{C-ax}{b}\end{align}$$

Om vi testar några olika värden på C får vi olika linjära funktioner. Vi ser med hjälp av figuren nedan att det minimala värdet på z kommer antas i något av hörnen på området (i det här fallet den röda linjen). Detta är det fundamentala resultatet i linjär optimering. På samma sätt kan vi söka det maximala värdet.

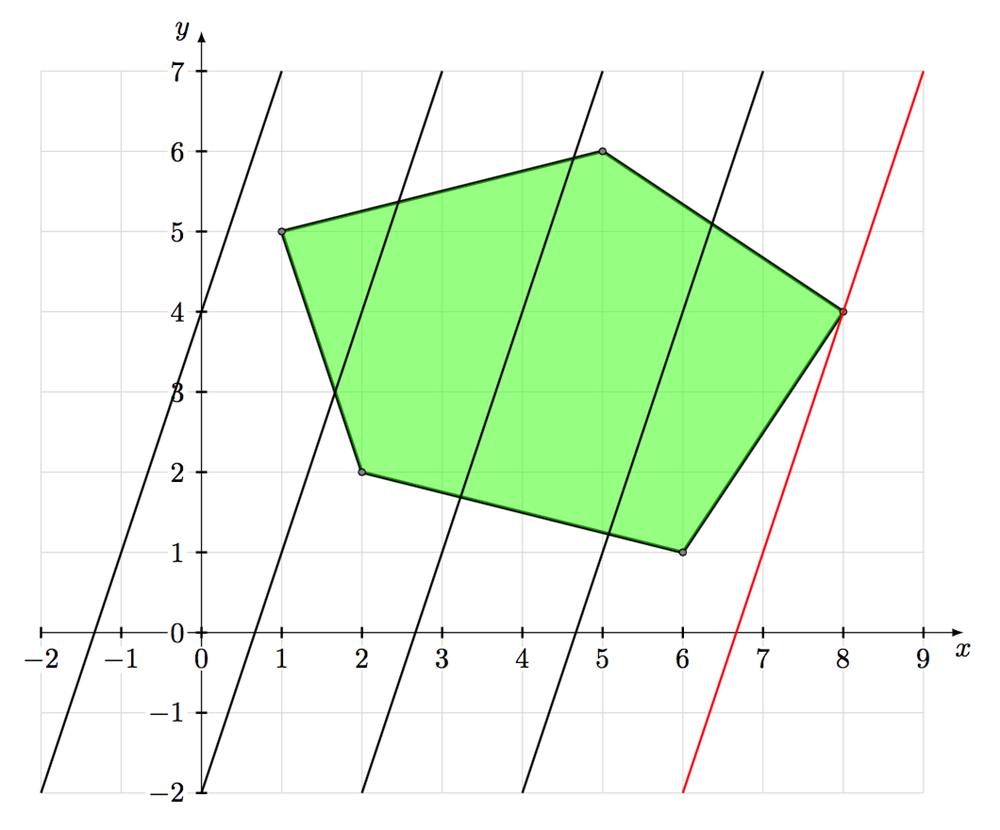
Sammanfattningsvis kan vi ställa upp en lista med 4 steg som vi kan följa för att lösa linjära optimeringsproblem i två dimensioner:

1. Definiera variablerna, det kan vara bra att göra det med x och y.
2. Definiera funktionen z, det vill säga den funktion vi vill optimera, med hjälp av x och y.
3. Definiera bivillkoren.
4. Nu optimerar vi funktionen z. Med hjälp av det fundamentala resultatet vi argumenterade för ovan vet vi att vi enbart behöver kolla hörnpunkterna i figuren. Vi stoppar alltså in hörnpunkterna i vår funktion z.

Ofta underlättar det om vi ritar upp området som definieras av bivillkoren. Detta gör det enklare att visualisera vilka punkter vi måste testa. 

Exempel

Ett företag säljer mobiltelefoner. De säljer en lite billigare variant för 2000kr och en lite dyrare för 6000kr. Att tillverka den billiga kostar 800kr/mobil och den dyra 2000kr/mobil.

Företaget vet att den billiga mobilen säljer åtminstone tre gånger bättre än den dyra. Hur många mobiler av varje sort ska företaget tillverka för att maximera sin vinst, om företaget har 120000kr i budget för att tillverka telefonerna?

Lösning:

Vi kallar den billiga varianten för \(x\) och den dyra för \(y\). Vår vinstfunktion beskrivs då av

$$z=2000x+6000y$$

Två av bivillkoren får vi enkelt, dessa är att \(x\geq 0\) och \(y\geq 0\), eftersom vi inte kan tillverka ett negativt antal telefoner.

Att företaget har 120000kr i budget för tillverkning av telefoner kan användas för att sätta upp bivillkoret

$$800x+2000y\leq 120000$$

Vi kan dela båda sidor med 800 och sedan flytta över x, vilket leder till

$$\begin{align}2,5y&\leq150-x\\&\iff\\y&\leq 60-\frac{x}{2,5}=60-\frac{2x}{5}\end{align}$$

Vidare vet vi att företaget vill tillverka åtminstone 3 gånger fler billiga telefoner, vilket leder till villkoret

$$y\leq \frac{x}{3}$$

Vår uppgift är alltså att maximera funktionen z=2000x+6000y så att:

$$\begin{align}\begin{cases} x&\geq 0\\y&\geq 0\\ y&\leq \frac{x}{3}\\y&\leq 60-\frac{2x}{5}\end{cases}\end{align}$$

Vi visualiserar detta med hjälp av en bild:

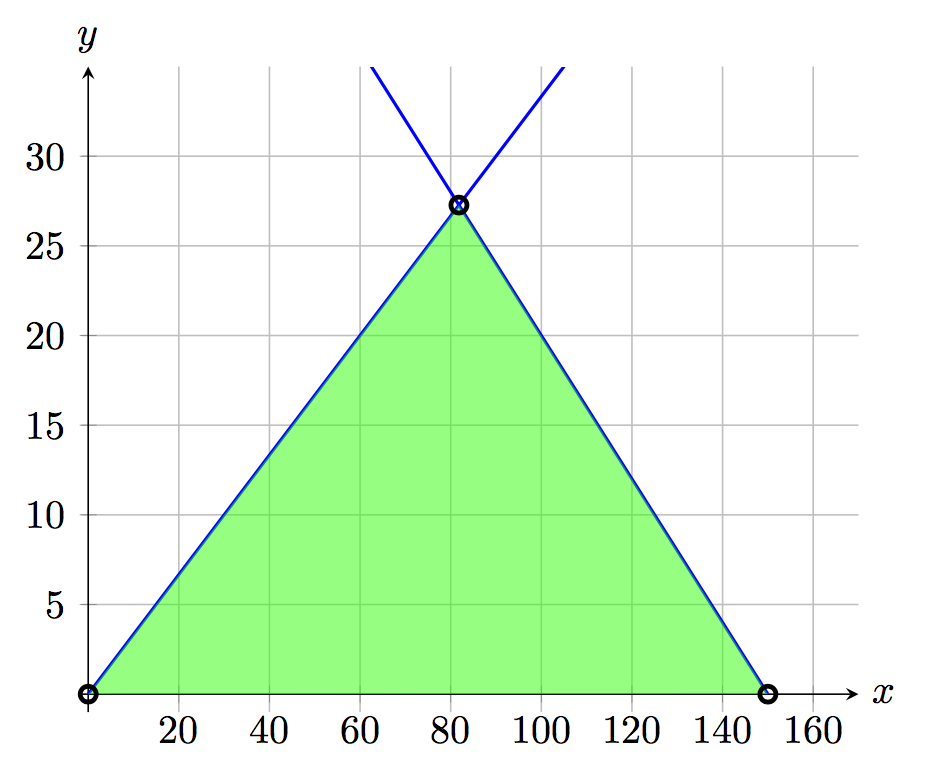
För att ta reda på den maximala vinsten testar vi alla hörnpunkter på det begränsade området.

Två av dessa punkter är enkla att se med hjälp av bilden, dessa är: \((x,y)=(0,0)\) och \((x,y)=(150,0)\).

Den tredje punktens x-värde kan vi enkelt hitta genom

$$\begin{align}\frac{x}{3}&=60-\frac{2x}{5}\\ & \iff \\ \frac{11x}{15}&=60\\ & \iff\\  x&=\frac{900}{11}\end{align}$$

Vilket ger punkten \((x,y)=(\frac{900}{11},\frac{300}{11})\).

Insättning i vinstfunktionen z ger:

$$\begin{align}z(0,0)&=0\\ z(150,0)&=2000\cdot150=300000\\z(\frac{900}{11},\frac{300}{11})&=2000\cdot\frac{900}{11}+6000\cdot\frac{300}{11}\approx 327273\end{align}$$

Alltså är det mest lönsamt om företaget producerar ungefär \(\frac{900}{11}\approx 82\) billiga telefoner och \(\frac{300}{11}\approx 27\) dyra telefoner.

Detta exempel är ett problem med enbart 2 variabler. I verkligheten är det ofta uppemot flera tusen, i vissa fall flera miljoner olika variabler med bivillkor. Att lösa sådana problem går inte att göra för hand. Däremot finns det algoritmer och metoder som gör att datorer kan lösa sådana problem effektivt.