Sannolikhetslära
Andrey Kolmogorov (1903-1987) var en rysk matematiker som gav många bidrag till matematiken. Ett av det mest uppmärksammade bidraget var hans definition på sannolikheter på utfallsrum. Denna definition kallas för Kolmogorovs axiomsystem, vilket vi går igenom i det här avsnittet.
Kolmogorovs axiomsystem
För att kunna tolka alla tecken i definitionen kan det vara bra att repetera mängdoperationer.
Definition:
En funktion \(P\) på händelser från utfallsrummet \(\Omega\) är en sannolikhetsfunktion om den uppfyller dessa tre villkor, även kallade axiom:
- För alla händelser \(H\subseteq \Omega\) så gäller att \(0\leq P(H)\leq 1\).
- \(P(\Omega)=1\), det vill säga sannolikheten av alla möjliga händelser är 1.
- \(P(H_1\cup H_2)=P(H_1)+P(H_2)\), om \(H_1\cap H_2=\emptyset\).
Om \(\Omega\) (utfallsrummet) är oändligt ersätter vi punkt 3 med
- Om \(H_1,\ H_2,\dots\) är en oändlig följd av händelser som är parvis oförenliga, det vill säga \(H_i\cap H_j=\emptyset\) för alla \(i\neq j\), så gäller:
$$P\left(\bigcup^\infty_{i=1}H_i\right)=\sum^\infty_{i=1}P(H_i)$$
I den första punkten ovan räcker det med kravet att \(P(H)\geq 0\), eftersom de andra punkterna implicerar att \(P(H)\leq 1\), vilket kan visas genom följande beräkningar:
Vi börjar med att visa monotonitet, som betyder att om \(H\subseteq B\) så gäller att \(P(H)\leq P(B)\).
Eftersom \(H\) är en delmängd av \(B\) kan vi skriva
$$B=H\cup (B\backslash H)$$
vilket betyder B=(H eller (B men inte H)).
Det är enkelt att se att H och (B\H) är disjunkta (de har inga gemensamma element). Därmed kan vi använda Kolmogorovs tredje axiom, vilket ger:
$$P(B)=P(H\cup (B\backslash H))=P(H)+P(B\backslash H)$$
Eftersom P(H) och P(B\H) båda är positiva (det första axiomet) gäller att
$$P(H)\leq P(B)$$
Eftersom \(H\subseteq \Omega,\ P(\Omega)=1\) och monotonitetsegenskapen gäller att
$$P(H)\leq P(\Omega)=1$$
vilket är det vi ville visa.
Komplement och additionssatsen
En direkt följd av definitionen ovan är följande, väldigt användbara, sats.
Komplement och additionssatsen: Om \(A\) och \(B\) är två godtyckliga händelser i ett utfallsrum \(\Omega\) så gäller följande:
- \(P(A^c)=1-P(A)\)
- \(P(\emptyset)=0\)
- \(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)
Bevis:
1. Eftersom hela utfallsrummet \(\Omega=A\cup A^c\) och att \(A\cap A^c=\emptyset\) får vi (av kolmogorovs tredje axiom) att:
$$P(\Omega)=P(A\cup A^c)=P(A)+P(A^c)$$
Subtrahera P(A) på båda sidor och kolmogorovs andra axiom ger:
$$P(A^c)=P(\Omega)-P(A)=1-P(A)$$
2. Eftersom \(A\cup\emptyset=A\) och \(A\cap\emptyset=\emptyset\) får vi:
$$P(A)=P(A\cup\emptyset)=P(A)+P(\emptyset)$$
vilket implicerar att \(P(\emptyset)=P(A)-P(A)=0\).
3. Vi börjar beviset med att skriva:
$$A\cup B=A\cup (B\cap A^c)$$
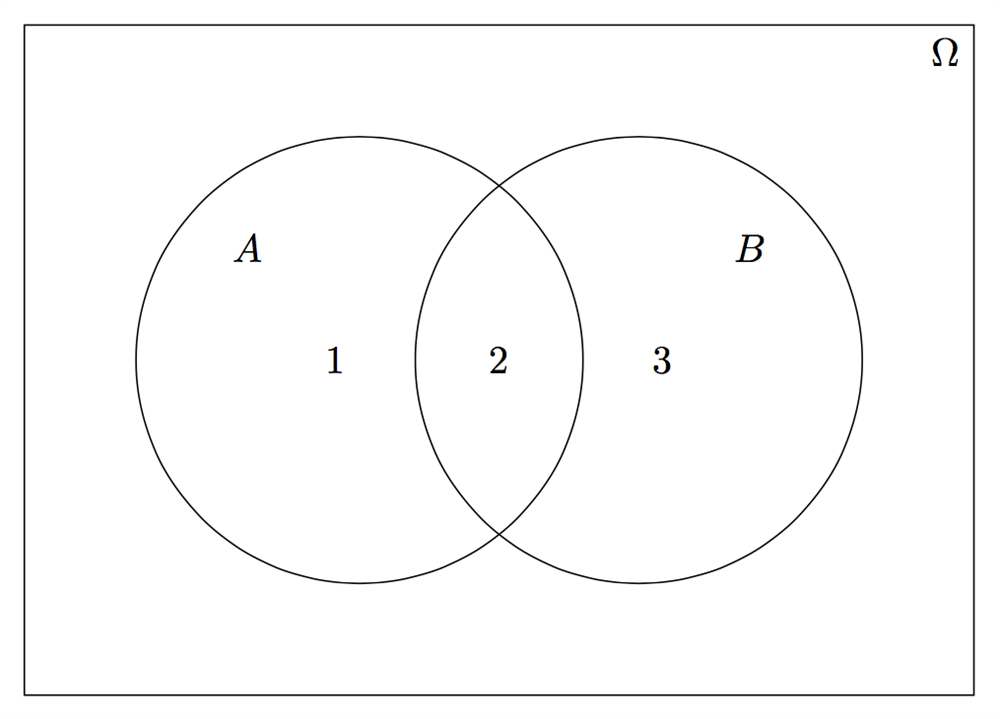
\(A\) och \(B\cap A^c\) är disjunkta, alltså är \(A\cap(B\cap A^c)=\emptyset\). Detta går enkelt att se med hjälp av venndiagrammet nedan. Mängden A är område 1 och 2, och området 3 är \(B\cap A^c\).
Vi kan nu använda oss av det tredje axiomet:
$$P(A\cup B)=P(A\cup (B\cap A^c))=P(A)+P(B\cap A^c)$$
Idén nu är att vi skriver om:
$$B=(B\cap A)\cup(B\cap A^c)$$
De två mängderna i H.L. är disjunkta, alltså kan vi använda oss av axiom tre igen
$$P(B)=P((B\cap A)\cup(B\cap A^c))=P(B\cap A)+P(B\cap A^c)$$
Lite omskrivning ger:
$$P(B\cap A^c)=P(B)-P(B\cap A)$$
Substituerar vi in detta får vi:
$$\begin{align}P(A\cup B)=P(A\cup (B\cap A^c))&=P(A)+P(B\cap A^c)\\&=P(A)+P(B)-P(B\cap A)\end{align}$$
vilket är det vi ville visa.
Vi ska nu visa hur vi kan använda denna sats med ett exempel
Exempel
Låt händelse \(A\)="Du drar ett ess ur en vanlig kortlek" och \(B\)="Du drar en spader".
a) Vad är sannolikheten att du inte drar ett ess?
b) Vad är sannolikheten att du drar ett ess eller en spader?
Lösning:
a) Eftersom \(A\)="Du drar ett ess" är \(A^c\) den sökta sannolikheten. Av satsen ovan får vi
$$P(A^c)=1-P(A)=1-\frac{4}{52}=\frac{12}{13}$$
b) Den sökta händelsen i det här fallet är \(A\cup B\). \(A\cap B\)="spader ess", och eftersom det bara finns ett sådant kort får vi
$$\begin{align}P(A\cup B)&=P(A)+P(B)-P(A\cap B)=\frac{4}{52}+\frac{13}{52}-\frac{1}{52}\\&=\frac{16}{52}=\frac{4}{13}\end{align}$$
Övning:
Bevisa Booles olikhet. Booles olikhet innebär att för två godtyckliga händelser, A och B, gäller:
$$P(A\cup B)\leq P(A)+P(B)$$
Komplement och additionssatsen (punkt 3) ger att:
$$\begin{align}P(A\cup B)=P(A)+P(B)-P(A\cap B)\end{align}$$
Eftersom \(P(A\cap B)\geq 0\), av Kolmogorovs första axiom, följer olikheten.
