Vektorer

I Matte 1-kursen lärde vi oss lite om vektorer. I det här avsnittet kommer vi lära oss mer om vektorer och hur vi räknar med dem.

En vektor kan representeras i koordinatform:

$$\vec{a}=(a_1,a_2,a_3)$$

Detta är ett exempel på en vektor i ett tredimensionellt, rätvinkligt koordinatsystem, även kallat ett linjärt rum eller vektorrum.

Inom matematiken behöver vi inte begränsa oss till två- eller tredimensionella rum. Denna studie av vektorer i två- och tredimensionella rum har utökats till n-dimensionella rum. Att studera vektorer i n-dimensionella rum kallas för linjär algebra.

Olika representationer

Som nämndes i stycket ovan kan en vektor representeras i koordinatform. I ett n-dimensionellt rum ser det ut såhär:

$$\vec{a}=(a_1,a_2,\dots,a_n)$$

Talen \(a_1,a_2,\dots,a_n\) kallas för komponenter. 

Arbetet med vektorer sker ofta tillsammans med matriser, som vi går igenom i nästa avsnitt. När vi jobbar med matriser kan det vara bra att representera vektorerna antingen som en kolonnvektor, eller en radvektor.

Kolonnvektorer ser ut såhär:

$$\begin{bmatrix}a_1\\a_2\\\vdots\\a_n\end{bmatrix}$$

och radvektorer:

$$\begin{bmatrix}a_1 & a_2 &\dots & a_n\end{bmatrix}$$

Som nämnts i tidigare kurser kan en vektor representeras med hjälp av enhetsvektorer, men detta bara om koordinatsystem är ett ortonormalt system (ON-system).

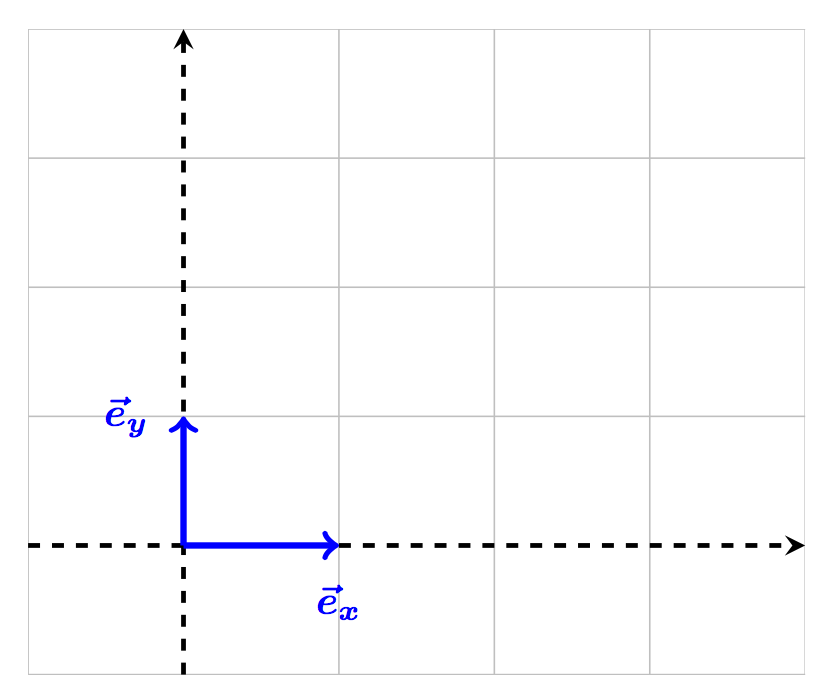
Ett ON-system är ett koordinatsystem som kan "spännas upp" av enhetsvektorer. Enhetsvektorer har längden ett och om enhetsvektorer sinsemellan är vinkelräta är rummet ortonormalt. Till exempel är \(\mathbb{R}^2\) ett ortonormalt system då det kan spännas upp av enhetsvektorerna \(\vec{e_x}=(1,0)\) och \(\vec{e_y}=(0,1)\):

Exempel

Vi skriver vektorn \(\vec{a}=(4,3,-2)\) med hjälp av enhetsvektorerna \(e_1=(1,0,0),\ e_2=(0,1,0)\) och \(e_3=(0,0,1)\) på följande sätt:

$$\begin{align}\vec{a}&=(4,3,-2)=4\cdot e_1+3\cdot e_2-2\cdot e_3\\&= 4\cdot(1,0,0)+3\cdot(0,1,0)-2\cdot(0,0,1)\end{align}$$

Normen av en vektor

Ibland är det bra att ta reda på längden av en vektor. Längden av en vektor brukar kallas för normen av vektorn och vi skriver

$$||\vec{a}||$$

I ett vinkelrätt vektorrum, det vill säga där koordinataxlarna är vinkelräta mot varandra, räknar vi ut normen av en vektor \(\vec{a}\) med hjälp av Pythagoras sats:

$$||\vec{a}||=\sqrt{a_1^2+a_2^2+\dots+a_n^2}$$

Normen av en vektor är alltid ett reellt tal.

Exempel

Beräkna normen för vektorn \(\vec{a}=(3,-2,4)\).

Lösning: 

$$\begin{align}||\vec{a}||=||(3,-2,4)||&=\sqrt{3^2+(-2)^2+4^2}\\&=\sqrt{9+4+16}\\&=\sqrt{29}\approx 5,39\end{align}$$

Skalärprodukt

Skalärprodukt (inner product på engelska) mellan två vektorer är en operation som bland annat definieras som:

$$\vec{a}\cdot\vec{b}=||\vec{a}||\ ||\vec{b}||\cos \theta$$

\(\theta\) i definitionen ovan är vinkeln mellan de två vektorerna. Om vi arbetar i ett ON-system kan skalärprodukten definieras som

$$\vec{a}\cdot\vec{b}=\sum_{k=1}^na_kb_k=a_1b_1+a_2b_2+\dots+a_nb_n$$

Vi går nu igenom räkneregler för skalärprodukten och formulerar det som en sats.

Sats: Låt \(\vec{a}\), \(\vec{b}\)  och \(\vec{c}\) vara vektorer i \(\mathbb{R}^2\) eller \(\mathbb{R}^3\). Då gäller

1. \(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}\)
2. \((\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}\)
3. \((k\vec{a})\cdot\vec{b}=k(\vec{a}\cdot\vec{b})\), där \(k\) är en konstant
4. \(\vec{a}\cdot\vec{a}\geq 0\)
5. \(\vec{a}\cdot \vec{a}=0\), om och endast om \(\vec{a}=0\)

Det är inte särskilt svårt att bevisa detta. Nedan visar vi beviset för punkt ett. De resterande punkterna kan bevisas på liknande sätt.

Bevis för 1: Enligt definitionen för skalärprodukt får vi:

$$\vec{a}\cdot\vec{b}=||\vec{a}||\ ||\vec{b}||\cos\theta=||\vec{b}||\ ||\vec{a}||\cos\theta=\vec{b}\cdot\vec{a}$$

Där den andra likheten håller eftersom den kommutativa lagen gäller för reella tal.

Den kommutativa lagen innebär att \(ab=ba\) för alla realla tal a och b.

Exempel

Beräkna vinkeln mellan vektorerna \(u=(3,4)\) och \(v=(5,12)\).

Lösning: Den här uppgiften går enkelt att lösa med hjälp av skalärprodukt. Eftersom vi arbetar i ett ON-system kan vi beräkna skalärprodukten genom

$$u\cdot v=(3,4)\cdot(5,12)=3\cdot5+4\cdot12=63$$

Vi vet även att 

$$u\cdot v=||u||\cdot||v||\cos \theta$$

Eftersom normen i det här fallet är samma som absolutbeloppet får vi

$$||u||=\sqrt{3^2+4^2}=\sqrt{25}=5$$

och

$$||v||=\sqrt{5^2+12^2}=\sqrt{169}=13$$

Alltså är

$$\begin{align}63&=5\cdot13\cos\theta\\&\iff\\\frac{63}{65}&=\cos\theta\\&\iff\\\theta&=\cos^{-1}\frac{63}{65}\approx 0,25\end{align}$$

Vinkeln mellan \(u\) och \(v\) är ungefär 0,25 radianer.