Cylindrar

I det här avsnittet ska vi lära oss om de geometriska figurer som vi kallar cylindrar. Det finns många cylinderformade föremål i vardagen, till exempel har ofta konservburkar och dricksglas formen av cylindrar.

Cylindrar

Den vanligaste typen av cylindrar som vi träffar på är så kallade raka, cirkulära cylindrar. Dessa cylindrar har två basytor i form av cirklar. Dessa basytor binds samman av en mantelyta.

Här nedanför kan du se hur en rak, cirkulär cylinder kan se ut.

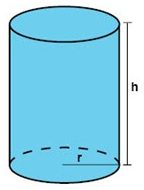
Volymen av en cylinder

När vi ska beräkna en cylinders volym, använder vi oss av samma formel som vi använde för prismor.

En cylinders volym är därför lika med dess basarea B multiplicerad med höjden h. Höjden h är lika med avståndet mellan de båda basytorna. Basytan har formen av en cirkel med radien r, så vi använder oss av formeln för en cirkels area för att beräkna basarean.

Volymen av en rak, cirkulär cylinder kan vi beräkna så här:

$$Volym=basarea\cdot höjd $$

$${V}_{rak,\,cirkulär\,cylinder}=B\cdot h=\pi{r}^{2}\cdot h$$

---

Hur stor är tonfiskburkens volym?

En vanlig konservburk med tonfisk kan ses som en cylinder. Basytan har formen av en cirkel med radien 4,25 cm och höjden på burken är 4 cm.

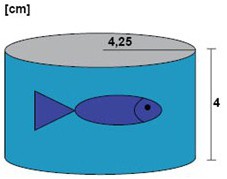
Lösningsförslag:

För att beräkna cylinderns volym börjar vi med att beräkna arean av basytan, som ju har formen av en cirkel.

Cirkelns radie är 4,25 cm, så vi får denna basarea:

$$ B=\pi{r}^{2}=\pi\cdot {4,25}^{2}\,(\approx 56,7\,{cm}^{2})$$

Cylinderns volym beräknar vi med hjälp av basarean och höjden 4 cm:

$$V=B\cdot h=\pi\cdot {4,25}^{2}\cdot 4\approx 227\,{cm}^{3}=227\,ml$$

Tonfiskburkens volym är ungefär 227 cm³, vilket är detsamma som 227 ml.

Videolektion

Här går vi igenom volym för en cylinder.

Här går vi igenom cylinder, vad det är och hur man beräknar volymen av en cylinder.

Här går vi igenom hur man beräknar arean av en cylinder.