Talmängder
I matematiken delar vi in talen i olika talmängder. En talmängd beskrivs med symbolen \(\{\}\). Vi börjar med de naturliga talen och utvidgar talområdet med olika typer av tal.
Naturliga tal
De naturliga talen är tal som vi normalt räknar med när vi ska räkna antal. Talmängden börjar med \(0\) och fortsätter mot större och större tal. \(0\) är varken positivt eller negativt och räknas till de naturliga talen som betecknas med:
$$\mathbb{N}=\left \{ 0,1,2,3,... \right \}$$
Negativa tal
Tal som är mindre än noll kallas för negativa tal. De börjar från \(-1\) och fortsätter mot mindre tal. Det finns ingen särskilt beteckning för de negativa talen.
Heltal
De naturliga- och de negativa talen bildar tillsammans heltal. Heltalen fortsätter växa både åt det negativa- och det positiva hållet. Mängden av heltalen betecknas med bokstaven \(\mathbb{Z}\) (från tyskans Zahlen, som betyder "tal").
$$\mathbb{Z}=\left \{ ..., -3, -2, -1, 0, 1, 2, 3,... \right \}$$
Rationella tal
Tal som är skriven på bråkform kallas för rationella tal. Villkoret för att ett tal ska vara rationellt tal är att både talet i täljaren och talet i nämnaren ska vara heltal. Dessutom får inte talet i nämnaren vara noll. Mängden av de rationella talen betecknas med bokstaven \(\mathbb{Q}\):
$$\mathbb{Q}=\left\{\texttt{alla tal}\;\frac{a}{b},\;\texttt{där alla}\;a\;\texttt{och}\;b\;\texttt{är heltal och}\;b\neq0\right \} $$
Detta innebär att alla heltal kan skrivas som ett rationellt tal, eftersom ett heltal \(a\) kan skrivas i bråkformen \(\frac{a}{1}\), och alla decimaltal som har ändlig decimalutveckling kan skrivas i bråkform. Exempelvis \(0,5=\frac{1}{2}\).
Irrationella tal
Alla tal som inte kan skrivas som ett bråk av två heltal kallas för irrationella tal. Exempelvis \(\sqrt2\) är ett tal som inte kan skrivas på bråkform. Ett annat exempel är \(\pi\) (pi) och talet \(e\).
Reella tal
Alla de rationella talen tillsammans med de irrationella talen utgör de reella talen. Mängden av de reella talen betecknas med bokstaven \(\mathbb{R}\).
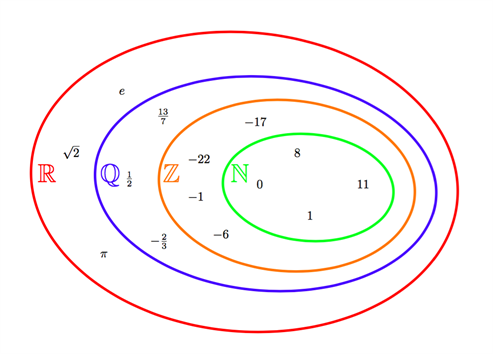
Talmängderna tillsammans
Talmängderna beskriver olika typer av tal. Mängderna och talen hänger ihop på följande sätt:
De naturliga talen \(\mathbb{N}\) ingår i heltalen \(\mathbb{Z}\) som ingår i de rationella talen \(\mathbb{Q}\) som ingår i de reella talen \(\mathbb{R}\).
På tallinjen kan man representera de reella talen enligt nedan:

Här går vi igenom olika typer av tal.
Här går vi igenom rationella tal och begreppen förlänga och förkorta.
Här förklarar vi skillnaden mellan rationella och irrationella tal.
- Mängd: Är en samling av objekt, exempelvis de olika talsorter (jämna-, udda- eller/och primtal). Men det kan vara något annat, t.ex. folkmängd eller antal elever på en klass/en skola.
- Heltal: \(\mathbb{Z}=\left \{ ..., -3, -2, -1, 0, 1, 2, 3,... \right \}\)
- Rationella tal: \(\mathbb{Q}=\{\text{alla tal}\;\frac{a}{b},\;\text{där}\;b\;\text{inte är noll}\}\).
- Irrationella tal: Tal som inte kan skrivas som bråk. Exempel: \(\pi\) och \(\sqrt2\).
- Reella tal: \(\mathbb{R}=\{\text{alla talmängder som nämnas ovan tillsammans}\}\).

Här lär man sig om de olika talmängderna och hur de hänger ihop. I genomgången beskrivs fyra talmängder:
- N naturliga tal
- Z hela tal
- Q rationella tal och
- R reella tal (de irrationella talen ingår i reella tal).

