Negativa tal

Negativa tal är det motsatta till positiva tal och de utgör en stor andel när vi räknar. Negativa tal har en del egenskaper och regler som man ska hålla i minnet när man räknar.

I avsnittet om talmängder kom vi fram till att heltalen utgörs av de naturliga talen \((0, 1, 2, …)\) och de negativa heltalen \((-1, -2, -3, …)\). I det här avsnittet ska vi titta närmare på negativa tal och de egenskaper som dessa tal har.

Negativa tal är tal som är mindre än noll. Vi skriver ett negativt tal på samma sätt som ett positivt tal, men med ett minustecken ("\(-\)") framför.

I vardagen stöter vi på negativa tal i olika sammanhang, bland annat i form av temperatur under nollstrecket på en termometer. Man kan till exempel säga att temperaturen ute en kall dag är \(-10°\)C, alltså \(10\) grader under noll (mätt i grader Celsius, förkortas C).

Exempel

Temperaturen är \(2°\)C mitt på dagen och sjunker \(5\)°C till kvällen:

$$2 – 5 = –3$$

Observera att minustecknen här har olika betydelser:

• Tecknet före \(5\) anger subtraktion.
• Tecknet före \(3\) anger att det är ett negativt tal.

Negativa tal på tallinjen

På en tallinje är de negativa talen placerade till vänster om talet noll:

Avståndet till noll är lika långt till exempel från \(+2\) som från \(-2\). På samma sätt är avståndet till noll lika långt för varje tal \(+a\) som för \(-a\). Man kallar talen \(a\) och \(-a\) motsatta tal, eftersom de befinner sig på lika avstånd till noll, fast det ena på den positiva sidan och det andra på den negativa sidan.

När vi räknar med negativa tal, är det vissa saker vi måste hålla i minnet. När vi lägger till positiva tal (adderar), rör vi oss till höger på tallinjen och när vi drar ifrån positiva tal (subtraherar) rör vi oss istället till vänster på tallinjen.

Om det är svårt att komma ihåg, kan det hjälpa att tänka på detta som temperaturen på en termometer. Om det är minusgrader ute och temperaturen sjunker, blir det ännu kallare, alltså drar vi bort grader. Då ökar antalet minusgrader eftersom vi kommer längre ner på skalan åt det negativa hållet.

Vi tittar på ett exempel:

$$-3-2=-5$$

På tallinjen ser det ut så här:

I det här fallet börjar vi vid \(-3\) och drar sedan bort \(2\). Alltså rör vi oss två steg åt vänster längs tallinjen från \(-3\) och hamnar i \(-5\). Är det temperatur vi mäter, så är det alltså samma sak som om temperaturen hade varit \(-3°\)C och sedan minskat med \(2°\)C, vilket ger den nya temperaturen \(-5°\)C.

Om temperaturen stiger däremot, blir det varmare, och det läggs till grader. Då ökar antalet grader och det blir mindre kallt eftersom antalet minusgrader blir färre.

Låt oss titta på ett exempel:

$$-3+4=1$$

På tallinjen kan vi se det som att vi går från \(-3\) till \(1\), så här:

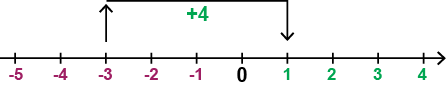
Vi börjar vid \(-3\) och rör oss fyra steg \((+4)\) till höger längs tallinjen och hamnar vid \(+1\). Med vårt temperaturexempel är det samma sak som om temperaturen hade varit \(-3°\)C och sedan ökade med \(4°\)C, vilket gav den nya temperaturen \(+1°\)C.

Addition och subtraktion

Ett begrepp som dyker upp i vardagslivet är ”skuld”.

Om du har \(100\) kronor på banken och \(25\) kronor i skulder, så har du bara \(75\) kronor att spendera. På samma sätt fungerar det att addera negativa tal:

$$100+(-25)=100-25=75$$

Att addera \(-25\) är alltså detsamma som att subtrahera \(25\).

Vi söker med andra ord hur stor differensen ”skillnaden” mellan talen är när vi subtraherar. Att addera två positiva tal däremot är detsamma som att se hur mycket talen är tillsammans.

Vi tar exemplet med banken igen men den här gången har man \(0\) kronor på kontot. Om man först får en skuld på \(100\) kronor sen får ytterligare en skuld på \(50\) kronor, då kan man addera de skulderna som negativa tal:

$$-100+(-50)=-150$$

Det betyder att man behöver \(150\) kronor för att nollställa sin ekonomi.

Ibland har vi situationer där vi ska subtrahera hela uttryck inom en parentes. Då får man komma ihåg att vara noga med eventuella teckenbyten för varje term som ingår i parentesuttrycket.

Här är ett exempel på hur det kan gå till:

$$100-(25+25)=100-25-25=50$$

I exemplet ovan har vi valt att inte beräkna uttrycket \((25 + 25)\) först, innan parentesen togs bort, utan låtit uttrycket stå kvar. Gör man så får man dock se till att vara noga med att alla termer i parentesuttrycket byter tecken. Vi kan också se att vi får samma resultat av uträkningen om vi direkt hade subtraherat \(50\) från \(100\), det vill säga räknat ut uttrycket inom parentesen först. För att undvika räknefel är det oftast en bra idé att räkna ut uttryck inom parenteser så långt det går, innan man går vidare med resten av uttrycket.

Allmänt kan vi sammanfatta dessa räkneregler som:

• \(a+(-b)=a-b\)
• \(a-(-b)=a+b\)
• \(a-(b+c)=a-b-c\)
• \((-a)+(-b)=-(a+b)\)

Multiplikation och division

När vi multiplicerar och dividerar med negativa tal måste vi ta hänsyn till tecken.

För multiplikation finns det två enkla regler:

Regel 1: Multiplikation mellan ett negativt tal och ett positivt tal, ger en negativ produkt:

$$(-3)\cdot 4=-12$$

\(3\) gånger \(4\) är ju \(12\), men eftersom vi har ett positivt och ett negativt tal blir svaret negativt och alltså \(-12\).

Symboliskt skrivs det som:

$$(-a)\cdot b=-ab$$

där \(a\) och \(b\) är positiva tal (\(-a\) är alltså ett negativt tal).

Regel 2: Multiplikation mellan två negativa tal, ger en positiv produkt:

$$(-3)\cdot (-4)=12$$

Med andra ord tar minustecknen ut varandra och svaret blir positivt.

Symboliskt skrivs det som:

$$(-a)\cdot (-b)=ab$$

där \(a\) och \(b\) är positiva tal (\(-a\) och\(-b\) är alltså negativa tal).

De två enkla reglerna för division:

Regel 1: Division mellan ett positivt och ett negativt tal ger en negativ kvot:

$$\frac{12}{-3}=-4$$

\(12\) dividerat med \(3\) är ju \(4\), men eftersom vi har ett positivt och ett negativt tal blir svaret negativt och alltså \(-4\).

Symboliskt skrivs det som:

$$\frac{a}{-b}=-c$$

där a är ett positivt tal och \(-b\) och \(-c\) är negativa tal.

Regel 2: Division mellan två negativa tal ger en positiv kvot:

$$\frac{-12}{-3}=4$$

Det vill säga att minustecken tar ut varandra och svaret blir positivt.

Symboliskt skrivs det som:

$$\frac{-a}{-b}=c$$

där \(-a\) och \(-b\) är negativa tal och \(c\) är ett positivt tal.

Kontrollera kvot

Ett sätt att kontrollera om man gjort rätt i en division, är att multiplicera nämnaren med kvoten. Är produkten av nämnaren och kvoten lika med täljaren, då har vi räknat rätt. Exempelvis kan vi ha att

$$\frac{12}{3}=4$$

För att se till att det är rätt kan vi multiplicera 3 (nämnaren) med 4 (kvoten) och får då produkten 12 (täljaren):

$$3\cdot 4=12$$

Sammanfattning av räkneregler för negativa tal

1. \(a+(-b)=a-b\)
2. \(a-(-b)=a+b\)
3. \(a-(b+c)=a-b-c\)
4. \((-a)+(-b)=-(a+b)\)
5. \((-a)\cdot b=-ab\)
6. \(a\cdot (-b)=-ab\)
7. \((-a)\cdot (-b)=ab\)
8. \(\frac{-a}{b}=-c\)
9. \(\frac{a}{-b}=-c\)
10. \(\frac{-a}{-b}=c\)

Till Toppen ⇧