Derivatan av sin(t) och cos(t)

Härled derivatan av derivatan av sin(t) och cos(t) genom att betrakta ett objekt som rör sig längs enhetscirkeln och vid tidpunkten t befinner sig i positionen (x(t),y(t))=(cos(t),sin(t)).

Vid tidpunkten t lämnar objektet enhetscirkeln i tangentens riktning och fortsätter i den i en tidsenhet. Härled derivatan av sin(t) och cos(t) genom att bestämma den position objektet befinner sig i vid tidpunkten t + 1.

Lösningsförslag:

Låt u vara lika med den tid som förflutit sedan objektet lämnat enhetscirkeln i tangentens riktning. Vi kan då beskriva objektets position enligt följande:

$$\\(x_{T}(t,\,u),\;y_{T}(t,\,u))=(x(t)+u\cdot x'(t),\;y(t)+u\cdot y'(t))\\$$

Om vi nu sätter u = 1, d.v.s. objektet förflyttar sig i tangentens riktning i en tidsenhet kan vi uttrycka den nya positionen i en figur enligt nedan:

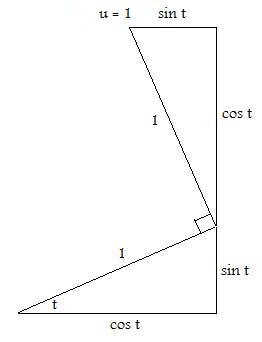
Vinkeln mellan trianglarna är 90˚ eftersom tangenten till en cirkel i en viss punkt alltid är vinkelrät mot linjen från origo till samma punkt.

Utifrån figuren kan vi bestämma objektets position för u = 1 eftersom trianglarna är likformiga.

$$\\(x_{T}(t,\,1),\;y_{T}(t,\,1))=(x(t)+1\cdot x'(t),\;y(t)+1\cdot y'(t))\\\\(x_{T}(t,\,1),\;y_{T}(t,\,1))=(x(t)+x'(t),\;y(t)+y'(t))\\\\(x_{T}(t,\,1),\;y_{T}(t,\,1))=(cos\,t+x'(t),\;sin\,t+y'(y))\\\\\left \{ enligt\;figuren \right \}\\\\(x_{T}(t,\,1),\;y_{T}(t,\,1))=(cos\,t-sin\,t,\;sin\,t+cos\,t)\\\\\left \{ identifiera\;x'(t)\;och\;y'(t) \right \}\\\\x'(t)=-sin\,t\\\\y'(t)=cos\,t\\\\V.S.V.\\$$