Några viktiga funktioners derivata
I Matte 3-kursen kom vi fram till deriveringsregler för ett antal vanligt förekommande funktionsuttryck. I det här avsnittet ska vi utöka vår uppsättning kända deriveringsregler med ytterligare några viktiga funktioners derivata.
Deriveringsregler för sin x och cos x
Tidigare i Matte 4-kursen har vi studerat de trigonometriska funktionerna.
$$f(x)=\sin\,x$$
och
$$f(x)=\cos\,x$$
Dessa används inom många olika områden och ofta är det då intressant att kunna beräkna dessa funktioners derivata.
Funktionen
$$f(x)=\sin\,x$$
har derivatan
$$f\,'(x)=\cos\,x$$
Funktionen
$$f(x)=\cos\,x$$
har derivatan
$$f\,'(x)=-\sin\,x$$
Dessa båda funktioners derivata kan härledas med hjälp av derivatans definition och numerisk undersökning av de gränsvärden som då uppkommer.
Vi ska nu räkna några exempel på derivering av sinus- och cosinusfunktioner
Derivera följande funktion.
$$f(x)=3\cos\,x$$
Denna funktion kan vi direkt derivera utifrån deriveringsregeln for cos x, men vi får inte glömma att behålla koefficienten 3.
Derivatan blir
$$f\,'(x)=3\cdot (-\sin\,x)=-3\sin\,x$$
Derivera följande funktion.
$$f(x)=\sin\,2x$$
Detta är en sammansatt funktion, som vi kan skriva som
$$f(x)=\sin\,(g(x))=f(g(x))=f(u)$$
där den yttre funktionen är
$$f(u)=\sin\,u$$
och den inre funktionen är
$$u=g(x)=2x$$
Denna sammansatta funktion bör vi kunna derivera med hjälp av kedjeregeln, så vi deriverar den yttre funktionen för sig och den inre funktionen för sig.
Den yttre funktionen
$$f(u)=\sin\,u$$
har derivatan (med avseende på u)
$$f'(u)=\cos\,u$$
Den inre funktionen
$$g(x)=2x$$
har derivatan (med avseende på x)
$$g'(x)=2$$
Med kedjeregeln får vi den sammansatta funktionens derivata
$$f\,'(x)=f'(g(x))\cdot g'(x)=$$
$$=(\cos\,2x)\cdot 2=$$
$$=2\cos\,2x$$
Derivera följande funktion.
$$f(x)=\cos\,\left (\frac{\pi}{4}-x \right )$$
Detta är en sammansatt funktion, som vi kan skriva som
$$f(x)=cos\,(g(x))=f(g(x))=f(u)$$
där den yttre funktionen är
$$f(u)=\cos\,u$$
och den inre funktionen är
$$u=g(x)=\frac{\pi}{4}-x$$
På samma sätt som i det föregående exemplet använder vi kedjeregeln för att derivera denna sammansatta funktion, så vi beräknar de yttre och inre funktionernas derivator.
Den yttre funktionen
$$f(u)=\cos\,u$$
har derivatan (med avseende på u)
$$f'(u)=-\sin\,u$$
Den inre funktionen
$$g(x)=\frac{\pi}{4}-x$$
har derivatan (med avseende på x)
$$g'(x)=-1$$
Med kedjeregeln får vi den sammansatta funktionens derivata
$$f\,'(x)=f'(g(x))\cdot g'(x)=$$
$$=-\sin\,\left ( \frac{\pi}{4}-x \right )\cdot (-1)=$$
$$=\sin\left ( \frac{\pi}{4}-x \right )$$
Deriveringsregler för exponentialfunktioner
I Matte 3-kursen introducerade vi talet e som den bas som gör att exponentialfunktionen
$$f(x)={e}^{x}$$
har derivatan
$$f\,'(x)={e}^{x}$$
Om vi skissar upp grafen till denna exponentialfunktion i ett rätvinkligt koordinatsystem, så kommer den att se ut så här:
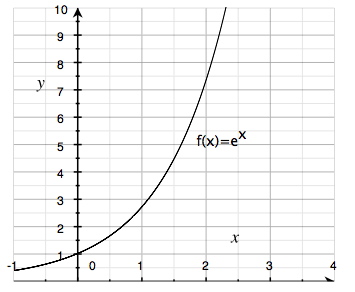
Som vi ser är denna exponentialfunktion strängt växande för alla värden på variabeln x, det vill säga dess derivata är alltid positiv. Det kan vi också komma fram till genom att studera uttrycket för funktionens derivata.
Tidigare har vi även kommit fram till att exponentialfunktionen med basen e på den mer allmänna formeln.
$$f(x)={e}^{kx} $$
där k är en konstant, har derivatan
$$f\,'(x)=k\cdot {e}^{kx}$$
I detta fall behöver dock inte funktionen vara strängt växande, då konstanten k ju får anta negativa värden. Om konstanten k antar ett negativt värde, så kommer funktionen att vara strängt avtagande - funktionens derivata kommer att vara negativ för alla värden på variabeln x.
Om exponentialfunktionens bas tillåts ha det godtyckliga värdet a, kan vi skriva funktionen som
$$f(x)={a}^{x}$$
Detta funktionsuttryck kan skrivas om med hjälp av den naturliga logaritmens definition, genom att sätta
$$a={e}^{\ln\,a}$$
och sedan byta ut basen i exponentialfunktion, så att vi får
$$f(x)={a}^{x}={({e}^{\ln\,a})}^{x}={e}^{(\ln\,a)\,\cdot x}$$
Skriven på detta sätt kan vi derivera funktionen på samma sätt som funktionen
$$f(x)={e}^{kx}$$
genom att
$$k=\ln\,a$$
Därför har en exponentialfunktion
$$f(x)={a}^{x}$$
derivatan
$$f\,'(x)=(\ln\,a)\cdot {e}^{(\ln\,a)\,\cdot x}$$
Eftersom
$$a={e}^{\ln\,a}$$
kan vi även skriva derivatan av funktionen med basen a som:
$$f\,'(x)=(\ln\,a)\cdot {a}^{x}$$
Denna funktions derivata stötte vi på i Matte 3-kursen, då vi undersökte nyttan med talet e.
Mer generellt kan man komma fram till att exponentialfunktionen
$$f(x)={a}^{kx}$$
där a är en godtycklig bas och k är en konstant, har derivatan
$$f\,'(x)=k\cdot (\ln\,a)\cdot {a}^{kx}$$
Deriveringsregler för logaritmfunktioner
Om vi har en funktion på formen
$$f(x)=\log\,x$$
eller
$$f(x)=\ln\,x$$
så kallar vi denna funktion en logaritmfunktion.
För dessa funktioner gäller generellt att de bara är definierade för positiva värden på den oberoende variabeln, så x > 0.
Logaritmfunktionen
$$f(x)=\ln(x)$$
där x > 0, har derivatan
$$f'(x)=\frac{1}{x}$$
Eftersom variabeln x bara får anta positiva värden kommer även derivatan alltid att anta positiva värden; därför är denna logaritmfunktion strängt växande för alla definierade värden på variabeln x.
Vi kan generalisera det ett steg till, om funktionen istället är
$$g(x) = \ln(kx)$$
så blir derivatan
$$g'(x) = \frac{k}{kx} = \frac{1}{x}$$
Vi kommer nu titta på två kortare bevis varför derivatan till naturliga logaritmen blir just \(f'(x)= \frac{1}{x}\)
Första beviset så kommer vi använda oss av gränsvärdet derivatans defintion, "tricket" för att det kommer funka kommer från att vi använder gränsvärdet för talet e och att \(\ln e = 1\) enligt definitionen. Vi kommer även använda oss av logaritmlagarna. Vi repeterar snabbt hur versionen för gränsvärdet för e vi kommer använda oss av ser ut
$$e= \lim_{h \to 0} (1+h)^{\frac{1}{h}}$$
Nu ställer vi upp gränsvärdet för derivatans definition och applicerar sen logaritmlagen för subtraktion och division.
$$\lim_{h \to 0 } \frac{\ln(x+h)-\ln(x)}{h} = \lim_{h \to 0} \frac{\ln (\frac{x+h}{x})}{h} = \lim_{h \to 0} \frac{\ln (1+\frac{h}{x})}{h}$$
Nu vill vi bryta ut \(\frac{1}{x}\) för vi vet redan att det är derivatan och visa att resten blir 1, så vi börjar med att skriva om nämnaren
$$\lim_{h \to 0} \frac{\ln (1+\frac{h}{x})}{h} = \lim_{h \to 0} \frac{\ln (1+\frac{h}{x})}{x\frac{h}{x}}=\lim_{h \to 0} \frac{1}{x}\frac{\ln (1+\frac{h}{x})}{\frac{h}{x}} $$
Vi kan flytta ut \(\frac{1}{x}\) eftersom det inte beror på h och sen kommer vi nyttja både att \(\frac{1}{\frac{h}{x}} = \frac{x}{h}\) och en till logaritmlag \(p\cdot\ln(a) = \ln(a^p)\)
$$\lim_{h \to 0} \frac{1}{x}\frac{\ln (1+\frac{h}{x})}{\frac{h}{x}} = \frac{1}{x} \lim_{h \to 0}\frac{x}{h}\cdot \ln(1+\frac{h}{x}) = \frac{1}{x} \lim_{h \to 0}\ln(1+\frac{h}{x})^{\frac{x}{h}}$$
Nu får vi använda oss av gränsvärdet för e som vi påmindes om i början och vi låter därför h gå mot 0 och då får vi
$$\frac{1}{x} \cdot \ln(e) = \frac{1}{x} \cdot 1 = \frac{1}{x} $$
Vilket skulle visas. (Detta är en vanlig fras att avsluta bevis med och ibland förkortar vi det till v.s.v.) Vi går vidare och kollar på nästa bevis, det är kortare men kan också anses knepigare.
Vi låter \(y= \ln(x) \) då får vi att \(e^y = e^{\ln(x)} = x\). Ekvationen nedan vill vi nu derivera på båda sidor med avseende på x.
$$e^y = x$$
Problemet som uppstår är att \(e^y\) inte innehåller något x, men det är inte heller en konstant. Vi jämför det med \(f(x) = e^{kx} \) om \(y=kx\) och den inre derivatan blir då
$$y'=k$$
$$f'(x) = k\cdot e^{kx} = y' \cdot e^y$$
Vi använder detta som det vi kommer få i VL när vi derivera \(e^y = x\), hela resultatet blir
$$y'\cdot e^y = 1 \cdot x^0 $$
$$y'\cdot e^y = 1$$
Målet är fortfarande att hitta derivatan av \(y= \ln(x)\) så vi försöker få \(y'\) ensamt och delar med \(e^y\)
$$y' = \frac{1}{e^y}$$
här byter vi tillbaka \(y\) mot \(\ln(x)\) och då får vi slutligen
$$y' = \frac{1}{x}$$
Vilket skulle visas!
Sammanfattning
Vi sammanfattar nu i en tabell derivatan av de funktioner vi stött på i detta avsnitt.
| Funktion | Derivata |
| \(\sin \, x\) | \(\cos \, x\) |
| \(\cos \, x\) | \(-\sin \, x\) |
| \(e^{kx}\) | \(k \cdot e^{kx}\) |
| \(a^{kx}\) | \(\ln \, a \cdot k \cdot a^{kx}\) |
| \(\ln \, x\) | \(\frac{1}{x}\) |
| Funktion | Derivata |
| \(\sin \, x\) | \(\cos \, x\) |
| \(\cos \, x\) | \(-\sin \, x\) |
| \(e^{kx}\) | \(k \cdot e^{kx}\) |
| \(a^{kx}\) | \(\ln \, a \cdot k \cdot a^{kx}\) |
| \(\ln \, x\) | \(\frac{1}{x}\) |
