Fler tillämpningar av integraler

I Matte 3-kursen lärde vi oss hur vi kan använda integraler för att beräkna arean mellan en kurva och x-axeln. I tidigare avsnitt såg vi också att det finns ett antal användbara räkneregler för integraler.

I det här avsnittet ska vi titta närmare på hur man kan tillämpa beräkning av integraler på problem som förekommer inom olika områden. Specifikt ska vi titta närmare på kopplingen mellan en funktion och dess primitiva funktion och hur denna kan användas för att lösa problem.

På det naturvetenskapliga området är det vanligt att man använder integraler för att bestämma storheter. Det kan till exempel röra sig om att man vill beräkna sträckan när man har en funktion för hastigheten eller att man vill beräkna hastigheten när man har en funktion för accelerationen.

Vi ska titta på ett exempel, där ett fordon färdas med en känd hastighet, som är en funktion av tiden. Det vi vill ta reda på är hur lång sträcka fordonet har färdats mellan två tidpunkter (mellan 5 sekunder och 10 sekunder från det att tiden börjar mätas).

Hur kan vi ta reda på detta med hjälp av en integralberäkning?

Hur hastigheten varierar beskrivs i denna situation med funktionen

$$v(t)=5\cdot {e}^{0,1t}$$

i intervallet 0 ≤ t ≤ 10 sekunder, vilket vi kan se i följande koordinatsystem.

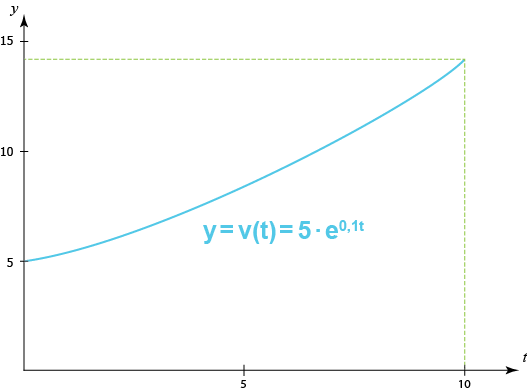
Ställer vi upp en integral

$$\int_{5}^{10}v(t)\,dt=\int_{5}^{10}(5\cdot {e}^{0,1t})\,dt$$

så innebär det att vi beräknar arean under kurvan i det intressanta intervallet.

Eftersom enheten för hastighet är meter per sekund och tidens enhet är sekunder, blir integralens enhet meter och anger sträckan fordonet färdats under tiden 5 s till 10 s med hastigheten v(t).

För att beräkna denna integral tar vi reda på den primitiva funktionen till v(t), vilken är V(t). Sedan Matte 3-kursen har vi en känd regel för hur vi kommer fram till den primitiva funktionen till en exponentialfunktion, nämligen att om

$$f(x)={e}^{kx}$$

så är den primitiva funktionen

$$F(x)=\frac{{e}^{kx}}{k}+C$$

Därför får vi

$$V(t)=\frac{5\cdot {e}^{0,1t}}{0,1}+C=50\cdot {e}^{0,1t}+C$$

Nu kan vi beräkna värdet av integralen:

$$s=\int_{5}^{10}(5\cdot {e}^{0,1t})\,dt=V(10)-V(5)=$$

$$=50\cdot {e}^{0,1\cdot 10}+C-(50\cdot {e}^{0,1\cdot 5}+C)=$$

$$=50\cdot {e}^{1}+C-50\cdot {e}^{0,5}-C=$$

$$=50\cdot e-50\cdot \sqrt{e}\approx53\,m $$

Sträckan som fordonet färdades mellan tidpunkterna t₁ = 5 s och t₂ = 10 s är alltså ungefär 53 m.

I tidigare avsnitt såg vi hur vi kunde beräkna rotationsvolymer och sannolikheter med hjälp av integraler. Andra exempel på storheter som vi kan bestämma med hjälp av integraler är:

• integralen av acceleration \(a(t)\) med standardenheten \(m/s^2\) ger oss hastighet \(v(t)\) i standardenheten \(m/s\).
• integralen av kraft \(f(x)\) med standardenheten Newton \(N\) ger oss arbete  \(W\) i standardenheten Newtonmeter \(Nm\).
• integral av tillväxthastighet ger antal. Exempelvis om vi har en funktion som ger oss tillväxthastigheten av en population av människor, bakterier eller annat så ger integralen av denna funktion antalet under ett intervall.