Polynomekvationer av högre grad

I tidigare avsnitt repeterade vi hur polynomekvationer av andra graden kan ha icke-reella lösningar, vilka vi kan uttrycka genom införandet av komplexa tal. Dessa lösningar på andragradsekvationer kan vi hitta med hjälp av de generella lösningsmetoderna kvadratkomplettering eller pq-formeln. Vi har även tidigare stött på metoder för att lösa vissa specialfall av polynomekvationer av högre grad.

I det här avsnittet ska vi studera lösning av polynomekvationer av högre grad än 2. Vi kommer att bekanta oss med faktorsatsen och använda oss av polynomdivision som ett mellanled i lösningen av polynomekvationer av högre grad.

Lösning av andragradsekvationer

Har vi en fullständig andragradsekvation så kan vi skriva om den som

$${x}^{2}+px+q=0$$

där \(p\) och \(q\) är reella tal.

Denna andragradsekvation kan vi lösa med bekanta metoder, såsom kvadratkomplettering eller pq-formeln, vilka vi gick igenom redan i Matte 2-kursen. Ibland kan vi även lösa andragradsekvationen grafiskt, men detta är inte fallet om den har icke-reella lösningar.

Skriva polynom i faktorform

Vissa specialfall av polynomekvationer av högre grad, till exempel tredjegradsekvationer som kan skrivas i formen

$${x}^{3}+a{x}^{2}+bx=0$$

där a och b är reella tal, kan vi redan lösa, genom att bryta ut faktorn x och sedan använda nollproduktsmetoden.

Vi får då

$$x\cdot ({x}^{2}+ax+b)=0$$

Detta innebär att antingen

$$x=0$$

eller

$${x}^{2}+ax+b=0$$

vilket ju är en andragradsekvation som vi kan lösa med till exempel pq-formeln.

Har vi en fullständig tredjegradsekvation som kan skrivas som

$${x}^{3}+a{x}^{2}+bx+c=0 $$

så kan vi skriva om polynomet i ekvationens vänsterled i faktorform så att vi får

$$(x-{a}_{1})\cdot (x-{a}_{2})\cdot (x-{a}_{3})=0$$

där \(a_1, a_2\) och \(a_3\) är rötter till ekvationen. Om vi sätter in \(x = a_1, x = a_2 eller \(x = a_3\), så kommer alltså ekvationens vänsterled att bli lika med noll.

Har vi till exempel tredjegradsekvationen

$${x}^{3}+{x}^{2}-10x+8=0$$

så kan vi skriva den i faktorform som

$$(x-1)\cdot (x-2)\cdot (x+4)=0$$

där ekvationens lösningar är \(x_1 = 1, x_2 = 2\) och \(x_3 = -4\). Att uttryckligen kunna skriva ekvationen på detta sätt förutsätter dock att vi känner till dess lösningar.

Faktorsatsen

Emellertid kan vi använda detta sätt att skriva en polynomekvation för att ta reda på okända lösningar, om vi på något sätt, till exempel genom testning eller grafiskt, kan ta reda på en eller flera lösningar till ekvationen.

Generellt kan vi skriva en polynomekvation som

$$p(x)=0$$

För något värde \(x = a\) sådant att \(p(a) = 0\), kan vi skriva polynomet i faktorform med \((x - a)\) som en ingående faktor, vilket ger oss

$$p(x)=(x-a)\cdot q(x)$$

för något polynom \(q(x)\).

Omvänt gäller även att om vi kan skriva ett polynom \(p(x)\) som

$$p(x)=(x-a)\cdot q(x)$$

där \(q(x)\) är något polynom, så gäller \(p(a) = 0\).

Dessa samband kallas faktorsatsen och denna sats kan vi använda oss av för att lösa polynomekvationer av högre grad än 2.

Har vi till exempel den polynomekvation av tredje graden som vi stötte på ovan,

$${x}^{3}+{x}^{2}-10x+8=0$$

men bara känner till en lösning på denna ekvation, säg \(x = 1\), så kan vi med hjälp av faktorsatsen skriva polynomet som

$${x}^{3}+{x}^{2}-10x+8=(x-1)\cdot q(x)$$

där \(q(x)\) är ett än så länge okänt polynom av grad 2.

Kan vi nu på något sätt ta reda på vad polynomet \(q(x)\) är, så kan vi hitta samtliga lösningar på vårt givna tredjegradspolynom.

Att finna polynomet \(q(x)\) kan vi göra med hjälp av olika metoder, till exempel polynomdivision.

Polynomdivision

Från faktorsatsen vet vi att om \(x = a\) är en lösning till ekvationen

$$p(x)=0$$

då är \((x - a)\) en faktor i \(p(x)\) och vi kan skriva \(p(x)\) som

$$p(x)=(x-a)\cdot q(x)$$

för något polynom \(q(x)\).

Vi kan skriva om detta samband som

$$q(x)=\frac{p(x)}{x-a}$$

vilket innebär att vi kan ta reda på \(q(x)\) genom att vi dividerar de båda polynomen i högerledet. Detta är vad vi kallar polynomdivision.

När vi ska dividera ett polynom \(p(x)\) med \((x - a)\), då följer vi i grunden samma regler som gäller för division av reella tal.

Har vi till exempel tredjegradspolynomet från tidigare enligt

$$p(x)={x}^{3}+{x}^{2}-10x+8$$

och den kända faktorn \((x - 1)\), då får vi kvoten \(q(x)\) som

$$q(x)=\frac{p(x)}{x-a}=\frac{{x}^{3}+{x}^{2}-10x+8}{x-1}$$

Denna kvot beräknar vi med valfri metod för division, oftast använder vi metoden liggande stolen. För att visa hur detta går till så visar vi först två exempel hur vi dividerar vanliga tal med hjälp av liggande stolen. Här vill vi dela \(\frac{51}{3}\) och då skrivs det ut så här:

Vi tar tiotal och ental var för sig. Vi börjar med tiotal och därför blir det vi gör först är att undersöka hur många gånger 3 går i 5 och det är en gång, därför skriver vi en etta (markerad röd i bilden) ovanför femman, för att visa att det är också tiotal. Sedan multiplicerar vi 1 med 3 och subtraherar det. 

(Egentligen är det att vi subtraherar 30, men eftersom vi tar det var för sig behöver vi inte skriva ut det).
Nu ska vi ta oss an ental, det vill säga dela 21 med 3 och får därför 7 som vi skriver ovanför. Multiplicerar 7 med 3 och subtraherar från det vi hade kvar. Det ser ut så här:

Detta säger oss att vi fick ingen rest eftersom vi fick en nolla längst ner, alltså gick divisionen jämt ut och \(\frac{51}{3}= 17\). Vi tittar på ett till exempel. 

Nu vill vi dividera 76 med 3. Vi ställer upp divisionen med liggande stolen så här:

Vi börjar med att dela 7 med 3och det går 2 gånger, därför skriver vi en tvåa ovanför sjuan. Sedan multiplicerar vi 3 med 2 och subtraherar det från 7. 

Nu ska vi dividera 16 med 3, det går 5 gånger, så vi skriver 5 ovanför. Sedan multiplicerar 3 med 5 och subtraherar detta från 16.

Från detta kan vi se att vi fick en rest och därför gick divisionen inte jämt ut. Alltså kan vi säga:

$$\frac{76}{3}= 25 + \frac{1}{3}$$ 

 $$76 = 25\cdot 3 + 1 $$

Nu ska vi ta det vi lärt oss och använda det för att dividera polynom. Vi ska dela polynomet \(x^2 + x -12\) med \(x-3\) och skriver därför upp dem så här:

Likt när vi hanterade tal, så tar vi en term i taget. Så vi börjar med att dela \(x^2\) med \(x\) och får ett \(x\) kvar och skriver det ovanför. Nu ska vi multiplicera \(x\) med hela polynomet vi delar med och subtraherar detta från \(x^2+x-12\).

Obs! Håll koll på att skriva rätt term under varandra. Vi kan till exempel inte subtrahera 12 med 3x.  

Därför får vi kvar detta polynom. Notera att eftersom det står minus framför parentesen får vi \(x-(-3x) = 4x\). 

Nu ska vi dela \(4x\) med \(x\) och får därför 4 och skriver denna ovanför. Sedan multiplicerar vi 4 med \((x-3)\) och subtraherar det. 

Resten blir noll och då kan vi dra flera slutsater med hjälp av faktorsatsen. 

$$\frac{x^2+x-12}{x-3}= x+4$$

eller 

$$x^2+x-12 = (x-3)(x+4)$$

och därför kan vi också dra slutsatsen att \(x=3\) är en rot till \(x^2+x-12\). Vi hittade även den andra roten \(x = -4 \). 

Vi tittar på ett sista avslutande exempel där vi använder liggande stolen för att lösa polynomekvationer av högre grad. 

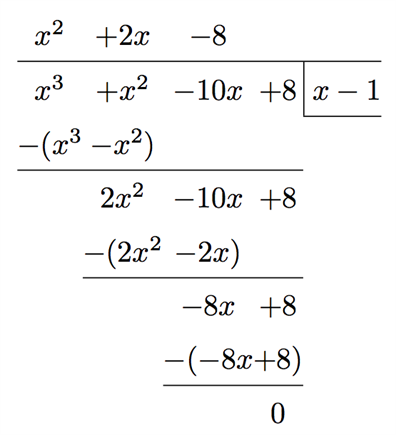
Polynomdivisionen fick resten 0, vilket innebär att divisionen gick jämnt ut. Detta kommer alltid att vara fallet då vi dividerar ett polynom \(p(x)\) med en känd faktor \((x - a)\). I det allmänna fallet med polynomdivision, kan det dock förekomma en restterm.

Den polynomdivision som vi utförde ovan resulterade i polynomet

$$q(x)={x}^{2}+2x-8 $$

Nu vet vi att följande gäller:

$$p(x)={x}^{3}+{x}^{2}-10x+8=$$

$$=(x-1)\cdot ({x}^{2}+2x-8)=0$$

Därför kan vi nu lösa

$$q(x)=0$$

till exempel med hjälp av pq-formeln, vilket ger oss rötterna

$$x=2\text{ och }x=-4$$

Samtliga rötter till ekvationen

$$p(x)={x}^{3}+{x}^{2}-10x+8$$

är alltså

$${x}_{1}=1$$

$${x}_{2}=2$$

$${x}_{3}=-4$$