Trigonometriska samband
I Matte 1- och Matte 3-kurserna har tidigare stött på de grundläggande trigonometriska sambanden. I det här och efterföljande avsnitt kommer vi att repetera en del av vad vi tidigare har lärt oss och även fördjupa oss inom trigonometrin.
I en rätvinklig triangel råder ett förutsägbart samband mellan någon av triangelns spetsiga vinklar och kvoten mellan två av triangelns sidor. Dessa samband har vi stött på tidigare:
$$\sin(v)=\frac{motstående\,katet}{hypotenusan} $$
$$\cos(v)=\frac{närliggande\,katet}{hypotenusan}$$
$$\tan(v)=\frac{motsående\,katet}{närliggande\,katet}$$
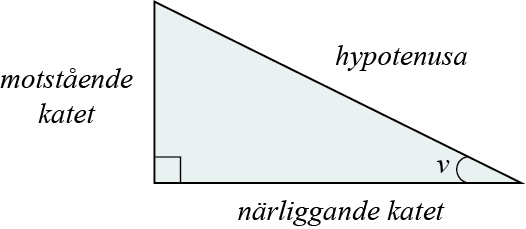
Värdet på dessa kvoter mellan två av triangelns sidor kommer att vara olika beroende på vilken storlek den spetsiga vinkeln har. För vissa storlekar på vinkeln kommer kvoten att bli ett exakt värde, som i många sammanhang är användbara att känna till.
Låt oss titta på några exempel
Beräkna längden på sidan x

Vi har en vinkel, hypotenusan och letar efter motstående sida och vi vet att
$$\sin v=\frac{motstående\: katet}{hypotenusan}$$
och då kan vi ställa upp den här ekvationen och lösa ut x
$$\sin(45^{\circ})= \frac{x}{42,5}$$
$$42,5 \cdot \sin(45^{\circ})= x$$
$$x = 30,0520...$$
Vi får att sidan x är 30 m lång. Nu kollar vi ett exempel när vi säker en vinkel och behöver använda arcsinus, arccosinus och arctangens.
Beräkna vinkeln v

I triangeln har fått värden på motstående sida och hypotenusan, så vi använder förhållandet
$$\sin(v) = \frac{28}{35}$$
$$\sin(v) = 0,8$$
Nu applicerar vi arcsin på båda sidor och får då i VL enbart v kvar
$$\arcsin(\sin(v))= \arcsin(0,8)$$
$$v = 53,13^{\circ}$$
Vinkeln v är ca \(53,13^{\circ}\)
Två viktiga trianglar
Vinklarna 30°, 45° och 60° ger oss exakta värden med sinus, cosinus och tangens. För att visa hur vi kommer fram till de här exakta värdena använder vi oss av två trianglar. Dessa kan vara bra att kunna rita upp istället för att minnas dessa utantill.
Vi börjar med en kvadrat med längd 1 och dela den på hälften längs diagonalen för att skapa en triangel och med Pythagoras sats kan vi beräkna att diagonalen blir \(\sqrt{2}\) längdenheter. Vi behåller ett hörn från kvadraten och där blir vinkeln rät, dvs 90° och de andra två blir delade på hälften och blir därför båda 45°.

Med hjälp av denna tringel kan vi få ut de exakta trigonometriska värdena för 45°
$$\tan 45 = \frac{1}{1} = 1$$
$$\sin 45 = \frac{1}{\sqrt2}$$
$$\cos 45 = \frac{1}{\sqrt2}$$
Vissa gillar inte att ha ett rottecken i nämnaren och skriver då gärna om \(\frac{1}{\sqrt 2} \) genom att förlänga med \(\sqrt 2\), det vill säga multiplicera med det i täljare och nämnare.
$$\frac{1}{\sqrt 2} = \frac{1\cdot \sqrt 2} {\sqrt 2 \cdot \sqrt 2} = \frac{\sqrt 2}{ \left( \sqrt 2 \right)^2} = \frac{\sqrt2}{2} $$
Nästa triangel så ritar vi upp en liksidig triangel med sidan 2 längdenheter, som vi delar på hälften längs höjden. Bottensidan blir då 1 längdenhet och med Pythagoras sats få ut att höjden blir \(\sqrt3\). Vinkeln som bildas mot höjden blir per automatik en rätvinkel och eftersom vi hade en liksidig var alla vinklar 60° från början och den som delades i hälften blir då 30°.

Utifrån den här triangeln får vi ut exakta trigonometriska värden för 30° och 60°
$$\sin(30^{\circ})= \frac{1}{2}$$
$$ \cos (30^{\circ}) = \frac{\sqrt 3}{2}$$
$$ \tan (30^{\circ}) = \frac{1}{\sqrt3}$$
$$ \sin (60^{\circ}) = \frac{\sqrt 3}{2}$$
$$ \cos (60^{\circ}) = \frac{1}{2}$$
$$ \tan (60^{\circ}) = \frac{\sqrt3 }{1} = \sqrt3$$
Vi sammanfattar detta avsnitt med de trigonometriska förhållandena i en rätvinklig triangel och exakta värdena för 30, 45 och 60°.
$$\sin v=\frac{motstående\: katet}{hypotenusan}$$
$$\cos v=\frac{närliggande\: katet}{hypotenusan}$$
$$\tan v=\frac{motstående\: katet}{närliggande\: katet}$$
| Vinkel \(v\) | \(\sin(v) \) | \(\cos(v) \) | \(\tan(v) \) |
| \(30^{\circ}\) | \(\frac{1}{2}\) | \(\frac{\sqrt 3}{2}\) | \(\frac{1}{\sqrt3}\) |
| \(45^{\circ}\) | \(\frac{1}{\sqrt 2}\) | \(\frac{1}{\sqrt 2}\) | \(1\) |
| \(60^{\circ}\) | \(\frac{\sqrt 3}{2}\) | \(\frac{1}{2}\) | \(\sqrt 3\) |
Här ser vi hur vi med hjälp av förhållandet mellan hypotenusan och en katet samt kunskaper inom trigonometri kan bestäma en vinkel i en triangel
- Rätvinklig triangel: en triangel där en av vinklarna är 90° grader (rät), bara en av vinklarna kan vara 90° grader för att skapa en triangel.
- Katet: en av de kortare sidorna i en rätvinklig triangel, sidorna ligger på varsin sida om den räta vinkeln och kallas flera kateter, eller en katet.
- Hypotenusa: den längsta sidan i en rätvinklig triangel, som är mittemot den räta vinkeln.
- Närliggande katet: givet en vinkel i en rätvinklig triangel så kallar vi katetern som ligger närmast, dvs bredvid vinkeln den närliggande kateten
- Motstående katet: givet en vinkel i en rätvinklig triangel så kallar vi katetern som ligger längst bort, dvs mitt emot vinkeln den motstående kateten
- Sinus: sinus av en vinkel ger oss förhållandet mellan motstående katet och hypotenusan
- Cosinus: cosinus av en vinkel ger oss förhållandet mellan närliggande katet och hypotenusan
- Tangens: tangens av en vinkel ger oss förhållandet mellan motstående och närliggande katet.
- Arcsin: om vi fått förhållandet mellan motstående katet och hypotenusan och vill hitta vinkeln använder vi arcsin, som är inversen till sinus
- Arccos: om vi fått förhållandet mellan närliggande katet och hypotenusan och vill hitta vinkeln använder vi arccos, som är inversen till cosinus
- Arctan: om vi fått förhållandet mellan motstående katet och närliggande katet och vill hitta vinkeln använder vi arctan, som är inversen till tangens
