Asymptoter
I det förra avsnittet undersökte vi hur vi kan skissa en funktions graf med hjälp av funktionens derivata. En intressant situation som ofta uppkommer då man ska skissa en funktions graf är att funktionen inte är definierad för alla variabelvärden. Detta stötte vi på redan i Matte 3-kursen, då vi undersökte funktioners gränsvärden.
I det här avsnittet ska vi bygga vidare på denna kunskap genom att lära oss mer om begreppet asymptoter och vilka konsekvenser dessa får för hur en funktions graf ser ut.
Vissa funktioner kan ställa till problem för oss då vi försöker att skissa deras grafer. Ett exempel på en sådan funktion är
$$f(x)=\frac{1}{x-1}+2$$
Något som vi direkt upptäcker är att funktionen inte är definierad för x = 1, eftersom nämnaren i kvoten med detta x-värde blir lika med noll. Alltså kan vi inte beräkna funktionsvärdet där x = 1. Däremot kan vi undersöka funktionsvärdena när vi rör oss längs kurvan närmare och närmare den punkt där x = 1, från antingen det negativa eller det positiva hållet.
Skissar vi grafen i ett rätvinkligt koordinatsystem så kommer den att se ut så här i närheten av x = 1.
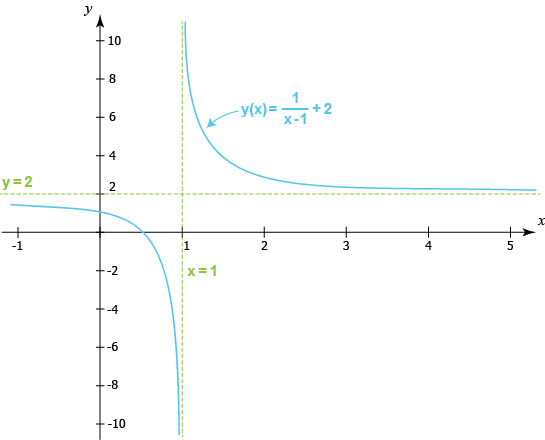
När vi närmar oss x = 1 från det negativa hållet kommer funktionsvärdet att bli mindre och mindre och anta värden som går mot minus oändligheten då vi kommer allt närmare x = 1. Då skriver vi funktionens gränsvärde som
$$\lim_{x \to 1-}f(x)=\lim_{x \to 1-}\left (\frac{1}{x-1}+2 \right )=-\infty$$
Närmar vi oss istället x = 1 från det positiva hållet, då kommer funktionsvärdet att bli större och större och anta värden som går mot plus oändligheten då vi närmar oss x = 1. I detta fall skriver vi funktionens gränsvärde som
$$\lim_{x \to 1+}f(x)=\lim_{x \to 1+}\left (\frac{1}{x-1}+2 \right )=\infty$$
Vad som händer här är att den första termen i vårt funktionsuttryck blir positivt eller negativt större och större ju närmare det odefinierade x-värdet vi kommer. Detta sker genom att nämnaren i den första termens kvot blir allt mindre och mindre (med positivt eller negativt tecken).
Vad vi har funnit här kan vi se som en rät, vertikal linje definierad av x = 1, som funktionens kurva kommer godtyckligt nära men aldrig skär. Denna räta linje benämner vi en asymptot. Just denna typ av asymptot, som utgörs av en vertikal linje och därför kan skrivas som ett specifikt x-värde, i det här fallet x = 1, kallas en vertikal asymptot.
Det finns även horisontella asymptoter, som på motsvarande sätt utgörs av horisontella räta linjer. I själva verket har vår exempelfunktion även en horisontell asymptot.
Den horisontella asymptoten hittar vi då vi befinner oss så långt bort som möjligt från det odefinierade x-värdet 1: när vi låter x-värdet närma sig negativa oändligheten eller positiva oändligheten. När vi låter x anta sådana värden, kommer konstanttermen 2 att bli alltmer dominerande i funktionsuttrycket i takt med att absolutbeloppet av kvoten
$$\frac{1}{x-1}$$
blir mindre och mindre. Denna krympande term kommer dock aldrig att anta värdet 0, vilket värde vi än låter variabeln x anta. Därför kommer heller aldrig funktionen att kunna anta värdet 2, men den kommer att kunna komma godtyckligt nära detta funktionsvärde, som därför utgör en horisontell asymptot.
Vi skriver detta som
$$\lim_{x \to \pm\infty}f(x)=\lim_{x \to \pm\infty}\left ( \frac{1}{x-1}+2 \right )=2$$
Allmänt gäller att grafen till en funktion f(x) har en vertikal asymptot där x = a om antingen
$$\lim_{x \to a-}f(x)=\pm\infty$$
eller
$$\lim_{x \to a+}f(x)=\pm\infty $$
På motsvarande sätt gäller att grafen till f(x) har en horisontell asymptot där y = b om antingen
$$\lim_{x \to -\infty} f(x)=b$$
eller
$$\lim_{x \to \infty} f(x)=b$$
- Definierad: Att en funktion är definierad i en punkt betyder att punktens x-värde ingår i funktionens definitionsmängd
- Funktionsvärden: värden som funktionen antar, oftast är det de som vi läser av på y-axeln i en graf
- Asymptot: en graf har en asymptot om det finns en linje som grafen närmar sig men inte kommer nudda eller skära
- Vertikal asymptot: en funktion f(x) har en vertikal asymptot där x = a om antingen
$$\lim_{x \to a-}f(x)=\pm\infty$$
eller
$$\lim_{x \to a+}f(x)=\pm\infty $$ - Horisontell asymptot: grafen till f(x) har en horisontell asymptot där y = b om antingen
$$\lim_{x \to -\infty} f(x)=b$$
eller
$$\lim_{x \to \infty} f(x)=b$$
