Trigonometri
Pythagoras sats anger det viktiga och användbara sambandet mellan de tre sidornas längder i en rätvinklig triangel. I det här avsnittet ska vi undersöka rätvinkliga trianglar, men denna gång ska vi hitta samband mellan längden på triangelns sidor och dess spetsiga vinklar.
De olika sidorna i en rätvinklig triangel benämns på olika sätt i relation till vinkeln som vi studerar:
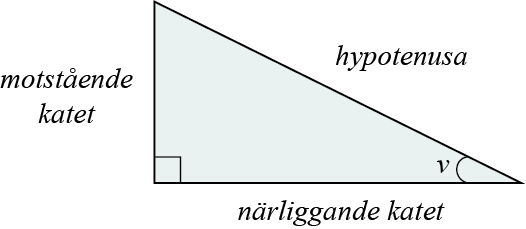
I den rätvinkliga triangeln här ovan studerar vi vinkeln \(v\) och benämner de olika sidorna i relation till denna vinkel. De två sidorna som möts i en \(90°\) vinkel kallas som bekant för kateter och den längre sidan som ligger mittemot den räta vinkeln kallas för hypotenusa. Den katet som ligger närmast vinkeln \(v\), kallas närliggande katet och den katet som ligger mittemot vinkeln \(v\), kallas för motstående katet. Detta är benämningar vi kommer att använda mycket framöver.
Trigonometriska funktioner
Sinus, cosinus och tangens är trigonometriska funktioner som anger förhållandet mellan längderna på en rätvinklig triangels sidor.
Ett sätt att förstå dessa trigonometriska funktioner är att det för en viss vinkel \(v\) grader alltid råder ett visst förhållande mellan den rätvinkliga triangelns sidor - det är detta förhållande man får ut när man beräknar sinus \(v\), cosinus \(v\) och tangens \(v\), men vilka sidor förhållandet gäller för skiljer sig åt mellan de olika trigonometriska funktionerna:
$$\sin v=\frac{\it\text{ motstående katet }}{\it\text{ hypotenusa }}$$
$$\cos v=\frac{\it\text{ närliggande katet }}{\it\text{ hypotenusa }}$$
$$\tan v=\frac{\it\text{ motstående katet }}{\it\text{ närliggande katet }}$$
För varje vinkel \(v\) finns alltså ett specifikt värde på sinus, cosinus och tangens. Detta värde anger alltså kvoten mellan två av längderna på triangelns sidor - vilka två sidor det rör sig om, det beror på vilken av de tre trigonometriska funktionerna vi använder, enligt formlerna ovan. Exempelvis kan vi beräkna alla förhållanden för triangeln nedan:

Här gäller det att:
$$\sin(53,1^\circ)=\frac{\it\text{ motstående katet }}{\it\text{ hypotenusa }}=\frac{4}{5}$$
$$\cos(53,1^\circ)=\frac{\it\text{ närliggande katet }}{\it\text{ hypotenusa }}=\frac{3}{5}$$
$$\tan(53,1^\circ)=\frac{\it\text{ motstående katet }}{\it\text{ närliggande katet }}=\frac{4}{3}$$
Sinus, cosinus och tangens är med andra ord bara olika namn för de kvoter som man kan ställa upp mellan en rätvinklig triangels sidor.
Låt oss försöka förstå oss på hur varje vinkel v ger ett specifikt värde på sinus, cosinus och tangens. I bilden nedan har vi ritat tre trianglar som alla har samma form, dvs. är likformiga. Vi har bara förstorat den ursprungliga triangeln i varje steg – först fördubblat den och sedan med en faktor \(3\).

Låt oss skriva upp en värdetabell för \(\sin v\), \(\cos v\) samt \(\tan v\) för respektive triangel. Minns definitionerna från innan:
| Trigonometrisk funktion | Triangel 1 | Triangel 2 | Triangel 3 |
| \(\sin(53,1^\circ)\) | \(\frac{4}{5}\) | \(\frac{8}{10}=\frac{4}{5}\) | \(\frac{12}{15}=\frac{4}{5}\) |
| \(\cos(53,1^\circ)\) | \(\frac{3}{5}\) | \(\frac{6}{10}=\frac{3}{5}\) | \(\frac{9}{15}=\frac{3}{5}\) |
| \(\tan(53,1^\circ)\) | \(\frac{4}{3}\) | \(\frac{8}{6}=\frac{4}{3}\) | \(\frac{12}{9}=\frac{4}{3}\) |
Vad för samband verkar det finnas mellan värdena för sinus, cosinus och tangens i respektive fall?
Det ser ut som att värdena är desamma, oberoende av storleken på triangeln. Med andra ord är de trigonometriska funktionernas värden enbart beroende av vinkeln i sig. De trigonometriska funktionerna kan ses som namn på de förhållanden som ställs upp mellan en rätvinklig triangels sidor. Alla likformiga, rätvinkliga trianglar har då samma förhållande mellan sina sidor; samma sinus, cosinus och tangens. Allt som skiljer dem åt är storleken på sidorna.
Dessa trigonometriska funktioner kan vi använda för att ta reda på den okända längden på en av en rätvinklig triangels sidor, om vi känner till längden på en av de andra sidorna och storleken på en av triangelns spetsiga vinklar. Eftersom rätvinkliga trianglar med samma vinkel är likformiga räcker det med att veta denna vinkel och storleken på en av sidorna för att bestämma den okända längden.
Beräkna en sidas okända längd
Säg att vi har en rätvinklig triangel med en känd vinkel på \(48°\), en hypotenusa med längden \(5,9\) cm och vi vill beräkna kateternas längder.
Till att börja med bör vi rita upp en figur, så att vi får överblick över triangelns sidor och vinklar, och därigenom minskar risken för att vi ska resonera fel:
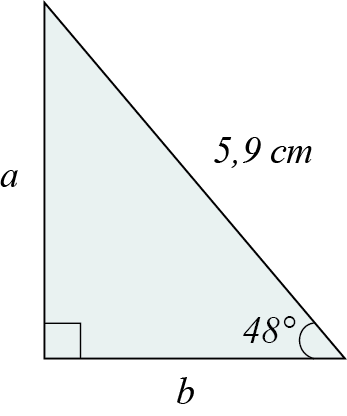
Utifrån den kända vinkeln är sidan b den närliggande kateten. Eftersom vi känner till längden på hypotenusan, så använder vi oss av cosinus-funktionen för att bestämma längden på sidan b.
$$\cos 48^\circ=\frac{b}{5,9}$$
$$5,9\cdot \cos 48^\circ=\frac{b}{5,9}\cdot 5,9$$
$$5,9\cdot \cos 48^\circ=b$$
En miniräknare kan på ett ungefär beräkna \(\cos(48 ̊)\). Det är dock viktigt att alltid ha en bild av vad det är man gör. Med en miniräknare får vi att:
$$5,9\cdot \cos 48^\circ \approx5,9\cdot 0,6691$$
vilket ger:
$$b\approx3,948\,\text{cm}$$
Tänk själv på om det även hade gått att använda sinusfunktionen för att bestämma sidan b.
Utifrån vår figur ser vi att sidan a är motstående katet, så vi använder oss av sinus-funktionen för att hitta längden på sidan a (i det här läget hade vi även kunnat använda oss av tangens-funktion, eftersom vi nu känner till längden på den närliggande kateten):
$$\sin 48^\circ=\frac{a}{5,9}$$
$$a=5,9\cdot \sin 48^\circ$$
$$a\approx5,9\cdot 0,7431$$
$$a\approx4,385\,\text{cm}$$
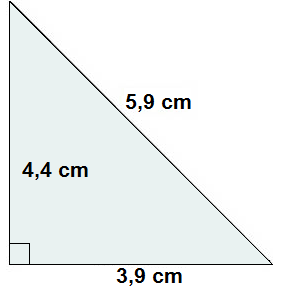
Längderna på de okända sidorna var alltså ungefär \(4,4\) cm (sidan \(a\)) och \(3,9\) cm (sidan \(b\)).
Beräkna en okänd vinkel
Frågan är om vi, givet en viss kvot, kan beräkna vilken vinkel det är som spänns upp av triangeln. Om vi exempelvis vet att \(\cos(v)=\normalsize{\frac{4}{5}}\), kan vi då veta vad vinkeln är?
För att hantera denna fråga introducerar vi det inversa värdet till sinus, cosinus och tangens. Inversen till sinus, cosinus och tangens är storleken på vinkeln \(v\) och skrivs antingen som arcsin, arccos och arctan eller på din miniräknare eller andra digitala hjälpmedel skrivs det som \(\sin^{-1}\), \(\cos^{-1}\) och \(\tan^{-1}\). En viktig sak att notera är att \(\sin^{-1}\) inte är samma sak som \(\normalsize{\frac{1}{\sin}}\). Dessa inversa trigonometriska funktioner kan vi alltså använda för att ta reda på hur stor en av de spetsiga vinklarna i en rätvinklig triangel är, om vi känner till längden på minst två av triangelns sidor eller mer konkret, deras förhållande.
Förenklat kan vi säga att inversa funktioner gör motsatsen till vad den vanliga funktioner gör. Om \(\tan x\) omvandlar en vinkel till en kvot så tar arctan en kvot och returnerar den korresponderande vinkeln.

De trigonometriska funktionerna sin, cos och tan, liksom de inversa trigonometriska funktionerna arcsin, arccos och arctan, finns alla förprogrammerade i vanliga grafritande miniräknare. Ofta kallas arcsin där \(\sin^{-1}\), och analogt för cos och tan. Men för att kunna använda dem på ett bra sätt behöver man veta vad de betyder och hur man bör göra för att man ska få ut rätt resultat.
Låt oss titta på ett exempel
Beräkna vinkeln mellan hypotenusan och sidan som är \(4\) längdenheter lång i följande rätvinkliga triangel:
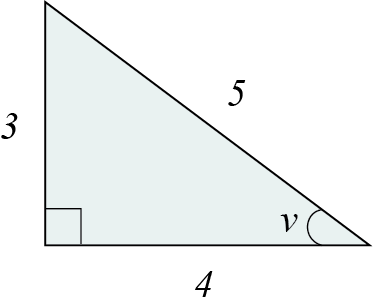
Vi börjar med att identifiera vinkeln som avses i texten: det är den spetsiga vinkeln till höger i triangeln. Detta innebär att sidan som är \(4\) längdenheter lång är den närliggande kateten och sidan som är \(3\) längdenheter lång är den motstående kateten.
Vi testar först att räkna ut vinkeln v med hjälp av cosinus-funktionen. Vi fyller i de värden vi känner till i formeln för cosinus:
$$\cos v=\frac{närliggande}{hypotenusa}$$
$$\cos v=\frac{4}{5}$$
För att lösa ut vinkeln v så använder vi den inversa funktionen (arccos):
$$v=\cos^{-1}\, \left ( \frac{4}{5} \right ) \approx 36,87 ^\circ$$
Alltså vinkeln v, vars cosinus värde är 4/5, är ungefär lika med 36,87 grader.
Nu testar vi att göra samma sak med hjälp av sinus-funktionen. Vi fyller i våra kända värden i formeln för sinus
$$\sin v=\frac{motstående}{hypotenusa}$$
$$\sin v=\frac{3}{5}$$
och så löser vi ut vinkeln v genom den inversa funktionen (arcsin):
$$v=\sin^{-1}\, \left ( \frac{3}{5} \right )\approx 36,87^\circ$$
Alltså vinkeln v, vars sinus värde är 3/5, är ungefär lika med 36,87 grader.
Till sist testar vi att göra samma sak med hjälp av tangens-funktionen:
$$\tan v=\frac{motstående}{närliggande}$$
$$\tan v=\frac{3}{4}$$
Vi löser ut vinkeln v genom att använda oss av den inversa funktionen (arctan) och får:
$$v=\tan^{-1}\,\left ( \frac{3}{4} \right ) \approx 36,87^\circ$$
Alltså vinkeln v, vars tangens värde är 3/4, är ungefär lika med 36,87 grader.
Som vi kan se får vi fram samma värde på vinkeln v oavsett vilken av de tre trigonometriska funktionerna vi väljer att använda, vilket är helt i sin ordning.
Här går vi igenom tangens och likformiga trianglar.
Här går vi igenom sinus och cosinus.
Här går vi igenom hur man beräknar en okänd vinkel med hjälp av trigonometriska funktionerna.
Här går vi igenom hur man beräknar sidas längd med hjälp av trigonometriska funktionerna.
Här går vi igenom några trigonometriska värden.
Här går vi igenom tangens invers.
Här går vi igenom inversen till sinus och cosinus.
Hjälpmedel
Här används grafräknaren Casio FX-CG20.
Se samma uppgift med grafräknaren Casio FX-9750GII.
Grafräknare av andra fabrikat har ungefär motsvarande funktionalitet.
- Rätvinklig triangel: En triangel där en av vinklarna är rät, det vill säga \(90°\).
- Spetsig vinkel: Är en vinkel som är större än noll grader \((0^\circ)\) och mindre än nittio grader \((90^\circ)\).
- Kateter: De sidor i en rätvinklig triangel som möts i den räta vinkeln.
- Hypotenusa: Är den längsta sidan i en rätvinklig triangel och motstående till den räta vinkeln.
- Trigonometriska funktion: Är en funktion som representerar förhållande mellan en rätvinklig triangels sidor.
