Räta linjens ekvation
Räta linjens ekvation beskriver ett linjärt samband mellan två variabler, \(y\) och \(x\). Linjen ritas som rak linje i ett koordinatsystem.
Räta linjens ekvation skrivs
$$y=kx+m$$
Där \(k\) och \(m\) är konstanter som avgör sambandet mellan variablerna \(x\) och \(y\). Konstanten \(k\) anger linjens lutning och \(m\) anger vid vilket värde som linjen skär y-axeln, då \(x=0\).
Exempel 1
Antag att konstanterna \(m=5\) och \(k=1\). Denna räta linjes ekvation är:
$$y=1\cdot x+5=x+5$$
Exempel 2
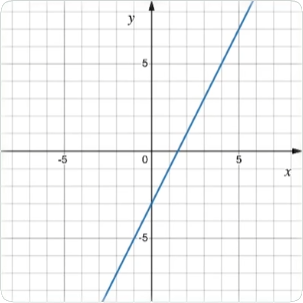
Den räta linjen \(y=2x+3\) har följande graf:

Linjen skär y-axeln vid \(y=3\), som vi kan läsa av via m-värdet, då \(x=0\).
Lutningen \(k\) hittas genom att studera hur stegen i x-led förhåller sig till stegen i y-led. För varje steg i x-led tas två steg i y-led för varje punkt längs linjen.

k-värdet \(2\) innebär en ökning av x-värdet med \(1\) och en ökning av y-värdet med \(2\). För varje steg \((+1)\) i x-led tas \(k\) steg i y-led.
Den räta linjen \(y=-2x+4\) har följande graf:

k-värdet \(-2\) innebär en ökning av x-värdet \((A-B)\) och en minskning av y-värdet \((B-C)\) med \(2\).
Konstanterna \(k\) och \(m\)
Konstanten \(k\) kallas riktningskoefficient och betecknar lutningen på linjen. Ett positivt k-värde ger en linje som lutar snett uppåt åt höger i koordinatsystemet, alltså att y-värdet blir större ju större värdet blir på den oberoende variabeln \(x\).

I figuren ovan ser vi i svart den konstanta linjen \(y=1\), i grönt \(y=x\), och i rött \(y=3x\).
Ett negativt k-värde ger en linje som lutar snett neråt åt höger, och att y-värdet blir mindre ju större värdet blir på den oberoende variabeln.

I figuren ovan ser vi den konstanta linjen \(y=1\) i svart, den minskande \(y=-x\) i grönt, och minskande \(y=-3x\) i rött.
När \(k=0\) så har linjen en horisontell lutning som är parallell med x-axeln. Notera att om \(k=0\) så kommer inte y-värdet att vara beroende av värdet på den oberoende variabeln – y-värdet kommer då att vara detsamma, konstant, oavsett av den oberoende variabelns värde. När k-värdet är \(0\), är \(y=0x+m\). Vilket är samma sak som \(y=m\).
Konstanttermen \(m\) bestämmer var linjen skär y-axeln. m-värdet motsvarar y-värdet i den punkten där \(x=0\), alltså där linjen skär y-axeln.
När m-värdet är positivt skär linjen y-axeln ovanför origo och när det är negativt skär linjen y-axeln under origo. När \(m=0\) går genom origo, dvs. punkten \((0,\,0)\).
Exempel 3
Ritar vi linjen \(y=x+5\) i exempel 1 skär y-axeln i punkten \((0,\,5)\), dvs. den punkt där \(x=0\) och \(y=5\).

Räkna ut lutning på en rät linje
Givet två punkter på linjen \((x_1, y_1)\) och \((x_2, y_2)\) så kan vi med följande formel räkna fram lutningen:
$$k=\frac{\text{Förändring i}\;y\text{-led}}{\text{Förändring i}\;x\text{-led}}=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$$
Exempel 4
Antag den räta linjen \(y=x+5\) med följande värdetabell.
| \(x\) | \(y\) |
| 0 | 5 |
| 1 | 6 |
| 2 | 7 |
| 3 | 8 |
| 4 | 9 |
Välj två godtyckliga punkter från tabellen, t.ex. \((0,\,5)\) och \((3,\,8)\). Vi sätter
$$(x_1, y_1)=(0, 5)\;\text{och}\;(x_2, y_2)=(3, 8)$$
Sätt in punkterna i formeln för att beräkna k-värdet:
$$k=\frac{y_2-y_1}{x_2-x_1}=\frac{8-5}{3-0}=\frac{3}{3}=1$$
Vi vet att detta stämmer, då funktionen har formen \(f(x)=x+5\), dvs. har \(k=1\).
Räkna ut var linjer skär \(y\)-axeln
Härnäst ska vi visa två metoder för att ta reda på \(m\)-värdet. Den ena metoden kallas för \(k\)-form och den andra kallas för enpunktsform.
Räkna ut linjens ekvation – 2 punkter givna
När vi har två punkter för en rät linje kan vi bestämma denna räta linjes ekvation \(y=kx+m\), genom att räkna ut \(k\)-värdet och \(m\)-värdet.
Exempel
Vi använder samma exempel som för \(k\)-värdet. Vi har räknat ut \(k\)-värdet till \(1\), med punkterna \((0,\,5)\) och \((3,\,8)\). Vi sätter in \(k\)-värdet i räta linjens ekvation för att lösa ut \(m\):
$$y=kx+m=1\cdot x+m=x+m$$
$$m=y-x$$
Vi vet två punkter på linjen, vi väljer någon av dem och sätter in i ekvationen. Vi får nu en ekvation med endast en variabel, vilket vi kan lösa. Exempelvis punkten \((3,\,8)\):
$$m=8-3=5$$
Konstanterna är nu beräknade till \(k=1\) och \(m=5\). Vår räta linjens ekvation är:
$$y=kx+m=1\cdot x+5=x+5$$
Linjens ekvation är \(y=x+5\)
Exempel
I följande geogebra - graf kan man studera lutningen (\(k\)-värde) och skärning med \(y\)-axeln (\(m\)-värde) genom att dra i glidarna och flytta punkterna (\(\color{Blue}{\text{A}}\) och \(\color{Blue}{\text{B}}\)) som beräknar \(k\).
Linjens ekvation i enpunktsform
När vi känner till \(k\)-värdet och en punkt för en rät linje kan vi bestämma denna räta linjes ekvation med hjälp av enpunktsformen:
$$y-y_1=k(x-x_1)$$
Exempel
Med samma exempellinje som tidigare har vi \(k=1\) och punkten \((x_1,y_1)=(3, 8)\). För alla punkter längs den räta linjen gäller sambandet
$$k=\frac{y-y_1}{x-x_1}\Rightarrow 1=\frac{y-8}{x-3}$$
Multiplicera upp nämnaren. Det ger räta linjens ekvation i enpunktsform.
$$1\cdot(x-3)=y-8$$
Räta linjens ekvation i \(k\)-form fås genom att lösa ut \(y\)
$$y=x-3+8=x+5$$
Proportionalitet
Om ekvationen \(y=kx+m\) saknar \(m\)-värde, dvs. \(m=0\), skrivs den räta linjen
$$y=kx$$
Detta specialfall kallas proportionalitet. Det betyder att de två variablernas förhållande är konstant. Man säger att \(y\) motsvarar en konstant multipel av \(x\). Om linjen är proportionell så är \(k=\frac{y}{x}\). (\(k\) kan vara positiv eller negativ)
T.ex. om man köper en vara som kostar \(a\) kr/kg beräknas kostnaden med \(y=ax\). \(x\)-axeln representerar antal kg av varan och kostnaden på \(y\)-axeln.
Räta linjens ekvation i allmän form
Den allmänna formen är \(ax+by+c=0\) där både \(a\) och \(b\) är skilda från \(0\). Om man dividerar båda sidor med \(b\) och flyttar \(ax\) till vänstersidan erhålles \(y=(-ax)/b-c/b\) det medför att
$$k=-\frac{a}{b}\, \text{och}\;m=-\frac{c}{b}$$
Här går vi igenom hur vi kan med hjälp av \(k\)-formen bestämma den räta linjens ekvation.
Här går vi igenom hur vi kan med hjälp av enpunktsformen bestämma den räta linjens ekvation.
Hjälpmedel
Här används grafräknaren Casio FX-CG20.
Se samma uppgift med grafräknaren Casio FX-9750GII.
Grafräknare av andra fabrikat har ungefär motsvarande funktionalitet.
- Linjär funktion: Är en funktion som har formen \(y=kx+m\), där där \(y=f(x)\).
- Riktningskoefficient: Det är värdet som bestämmer räta linjens lutning.
- Variabel: Är ett okänt värde som beskriver olika saker, t.ex. antal elever, temperaturer, kön, ålder osv.
- Origo: Är punkten med koordinat \((0,\,0)\), där axlarna möts och värdet är \(0\) på både \(x\) och \(y\).
- Proportionalitet: När sambandet mellan två variabler är konstant.
Räta linjens ekvation
Här går vi genom teorin om räta linjens ekvation y = kx + m. Det finns tre olika fall och vi går genom dem:
- \(k > 0\)
- \(k = 0\)
- \(k < 0\)
Bestäm ekvationen
a) Bestäm ekvationen för en rät linje som går genom origo och punkten (2, 6)
b) Bestäm ekvationen för en rät linje som går genom origo och punkten (-3, 12)
Ange \(k\) och \(m\)
Ange värdet på \(k\) och \(m\) till följande räta linjer
a) \(y = 2(x - 5)\)
För nedanstående exempel, se länk.
b) \(3y = -3(2x - 4) + 3\)
c) \(y = 4(ax + b)\)
Bestäm linjernas k-värde, m-värde och linjernas ekvationer
Del 1:
För del 2, 3 och 4, se länk.
Bestäm linjens ekvation
Rita en linje som går genom punkten (-2,5) och har lutningen -2.
Bestäm linjens ekvation.
Bestäm linjens ekvation algebraiskt
1. En rät linje med lutningen 3 går genom punkten (2,5). Bestäm linjens ekvation algebraiskt.
2. En rät linje går genom punkterna (-10,8) & (4,1)
Proportionalitet - teori
$$y = kx \;\;(m=0)$$
Bestäm ekvationen
Bestäm ekvationen för en rät linje som går genom origo och punkten för en rät linje som går genom origo och punkten (2, 6)
För (-3, 12), se länk.