Skillnad mellan dragning med och utan återläggning
Du ska undersöka skillnaden mellan dragning med och utan återläggning. Urnan innehåller 4 röda kulor och 6 svarta kulor. Du gör tre dragningar, med och utan återläggning.
a) Gör ett träddiagram och markera sannolikheterna.
b) Beräkna P(3 röda)
c) Beräkna P(2 svarta, 1 röd)
d) Jämför de 2 fallen
Fall 1 (dragning med återläggning):
a) Träddiagrammet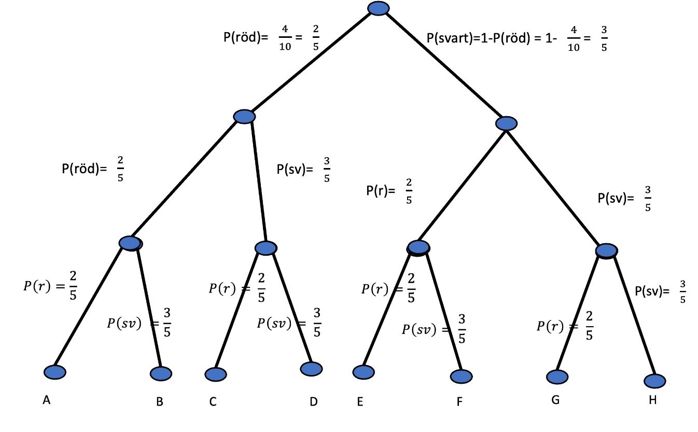
b) P(3 röda) = P(A) \(=\dfrac{2}{5} \cdot \dfrac{2}{5} \cdot \dfrac{2}{5} = \dfrac{8}{125} = 0,64 \)
c) P(2 svarta, 1 röd) = P(D) + P(F) + P(G) =
\[= \frac{2}{5}\cdot \frac{3}{5}\cdot \frac{3}{5} + \frac{3}{5}\cdot \frac{2}{5}\cdot \frac{3}{5} + \frac{3}{5}\cdot \frac{3}{5}\cdot \frac{2}{5} = 3\cdot \frac{2}{5}\cdot \frac{3}{5}\cdot \frac{3}{5} =\] \[= \frac{54}{125} = 0,432\]
Fall 2 (utan återläggning):
a) Träddiagrammet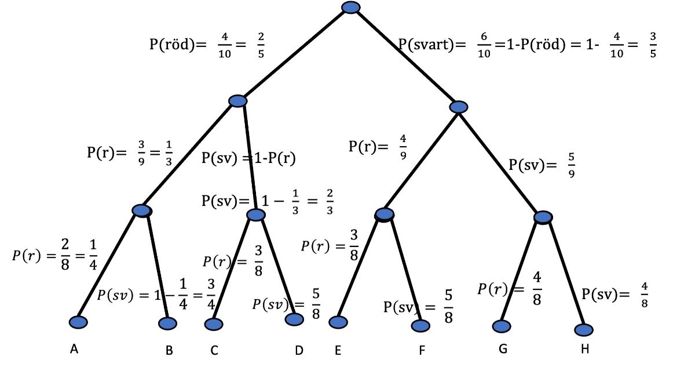
b) P(3 röda) = P(A) \(=\dfrac{2}{5} \cdot \dfrac{1}{3} \cdot \dfrac{1}{4} = \dfrac{2}{60}= \dfrac{1}{30} \approx 0,033 \)
c) P(2 svarta, 1 röd) = P(D) + P(F) + P(G) = \[= \frac{2}{5}\cdot \frac{2}{3}\cdot \frac{5}{8} + \frac{3}{5}\cdot \frac{4}{9}\cdot \frac{5}{8} + \frac{3}{5}\cdot \frac{5}{9}\cdot \frac{4}{8} = \frac{1}{6}+\frac{1}{6}+\frac{1}{6} =\] \[=\frac{3}{6} = \frac{1}{2} = 0,5\]
d) Jämförelse:
P(3 röda, Fall 1) \(>\) P(3 röda, Fall 2)
P(2 svarta, 1 röd, Fall 2) \(>\) P(2 svarta, 1 röd, Fall 1)
Svar:
a) Se träddiagrammen
b) P(3 röda, Fall 1) = 0,064 och P(3 röda, Fall 2) ≈ 0,033
c) P(2 svarta, 1 röd, Fall 1) = 0,432 och P(2 svarta, 1 röd, Fall 2) = 0,5
d) P(3 röda, Fall 1) \(>\) P(3 röda, Fall 2)
P(2 svarta, 1 röd, Fall 2) \(>\) P(2 svarta, 1 röd, Fall 1)
