Uppgift 4

På tallinjen finns sex punkter A-F markerade:

Varje tal nedan motsvaras av en markerad punkt på tallinjen.

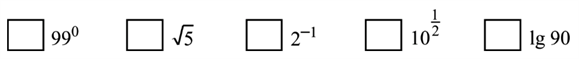
Para ihop vart och ett av talen med en punkt på tallinjen genom att skriva rätt bokstav A-F vid rätt tal.

Lösningsförslag

Vi tittar på varje tal för sig och avgör vilken punkt det tillhör:

\(99^0=1\implies 99^0=C\).

\(\sqrt{5}\), för att få ut ett ungefärligt värde på detta tal utnyttjar vi att vi redan vet \(\sqrt{4}=2\) och \(\sqrt{9}=3\), vilket betyder att \(2<\sqrt{5}<3\). Detta ger oss att \(\sqrt{5}=E\).

\(2^{-1}=\frac{1}{2}=0,5\implies 2^{-1}=B\).

\(10^{\frac{1}{2}}=\sqrt{10}\). Vi nämnde ovan att \(\sqrt{9}=3\), vilket betyder att \(\sqrt{10}\) är lite större än 3. Detta ger oss att \(10^{\frac{1}{2}}=F\).

\(\lg90\), för att få ett ungefärligt värde på detta tal utnyttjar vi att vi redan vet att \(\lg10=1\) och \(\lg100=2\), vilket betyder att \(1<\lg90<2\). Detta ger oss att \(\lg90=D\)

Svar:
\(99^0=C\)
\(\sqrt{5}=E\)
\(2^{-1}=B\)
\(10^{\frac{1}{2}}=F\)
\(\lg90=D\).

Uppgiften är hämtad ur "Kursprov Matematik 2c, vårterminen 2015" - Ladda ner provet här.