Polynom

Ett polynom är ett algebraiskt uttryck som kan användas som en matematisk modell för att beskriva olika situationer. Vi har tidigare stött på polynom och i det här och följande avsnitt ska vi lära oss mer om hur vi kan använda polynom när vi räknar, och vilka egenskaper polynom har.

Polynom består av variabler (till exempel x, y, z) och konstanter (till exempel 3, 17, -2) som har kombinerats genom de tre räknesätten addition, subtraktion och multiplikation. De variabeltermer som ingår i ett polynom får endast ha positiva heltalsexponenter. Det innebär att följande tre uttryck alla är polynom:

$$x^2+3x-1$$

$$-3x+2$$

$$2x^4-5x^3-x+7$$

Ett algebraiskt uttryck där variabeltermerna har exponenter som inte är positiva eller som inte är heltal, är därför inte heller ett polynom.

Polynoms gradtal

När vi ska beskriva ett polynom, anger vi ofta polynomets gradtal, med vilket vi menar den största positiva heltalsexponenten som någon av de ingående variabeltermerna har.

I vårt exempel ovan med bollens hastighet hade vi ett förstagradspolynom eftersom variabeln i termen 9,81t har exponenten 1 (när vi skriver "t" menar vi ju i själva verket "t¹", så exponenten är lika med 1). Just detta polynom hade bara en variabelterm, men ofta har polynom fler än en term.

Vi inledde detta avsnitt med tre exempel på polynom, som vi nu kan återvända till och ange gradtalen för.

Polynomet:

$$x^2+3x-1$$

är ett andragradspolynom, eftersom den största exponenten som någon variabelterm har är 2 (termen x²).

Vidare är

$$-3x+2$$

ett förstagradspolynom, då den största exponenten hos den enda variabeltermen är 1 (termen -3x).

På motsvarande sätt är polynomet

$$2x^4-5x^3-x+7$$

ett fjärdegradspolynom, eftersom vi har en variabelterm vars exponent är 4 (termen 2x⁴).

Variabeltermer av olika grad

Samma räknelagar gäller för polynom som för "vanliga" tal. Något som dock är viktigt att komma ihåg när vi räknar med polynom är att variabeltermer av olika grad inte kan läggas ihop med varandra hur som helst. Det är med andra ord till exempel stor skillnad på variabeltermerna x² och x³, eftersom

$$x^{2}=x\cdot x$$

$$x^{3}=x\cdot x\cdot x$$

vilket innebär att x³ är x gånger större än x².

Har vi ett polynom som består av variabeltermer av olika gradtal, så skriver vi dessa termer var för sig, ordnade efter termernas gradtal.

I följande exempel ser vi hur vi kan ordna variabeltermer av olika gradtal

$$x^{3}+2x+3x^{3}-x=(x^{3}+3x^{3})+(2x-x)=4x^{3}+x$$

(Parenteserna som vi tog med i beräkningen ovan är egentligen överflödiga, men vi tog med dem för att göra det tydligare att det rör sig om variabeltermer av samma gradtal.)

Vi adderar och subtraherar alltså variabeltermerna med de termer som har samma gradtal. Därigenom kan vi förenkla polynom.

Multiplikation med polynom

Vid multiplikation av polynom så är det viktigt att komma ihåg regeln att alla ingående termer i den ena polynomfaktorn ska multipliceras med alla ingående termer i den andra polynomfaktorn.

Vi tittar på följande exempel på multiplikation med polynom

$$2x\cdot (4+3x)$$

så är det sätt som vi beräknar denna produkt en tillämpning av den distributiva lagen, som vi stött på i samband med vår genomgång av heltalens egenskaper.

Den distributiva lagen, tillämpad på faktorn a och de i den andra faktorn ingående termerna b och c, säger oss att följande samband gäller:

$$a\cdot (b+c)=a\cdot b+a\cdot c$$

Jämför vi detta samband med den produkt som vi ska beräkna, så får vi i vårt exempel följande: a = 2x, b = 4, och c = 3x.

Vi ska alltså beräkna summan av 2x gånger 4 plus 2x gånger 3x. Polynomet som står utanför parentesen (2x) ska multipliceras med var och en av termerna i det polynom som står inom parentesen (4 + 3x).

Vi får därför:

$${\color{Blue} {2x}}\cdot ({\color{Red} {4+3x}})=$$

$${\color{Blue} {2x}}\cdot{\color{Red} {4}}+{\color{Blue} {2x}}\cdot {\color{Red} {3x}}=$$

$$8x+6x^{2}$$

Här kan vi också lägga märke till att det polynom som vi fick när vi räknade ut produkten av de två ursprungliga förstagradspolynomen blev ett andragradspolynom.

När vi multiplicerar med polynom är det viktigt att komma ihåg att plus- och minustecknen hör ihop med den term som står direkt till höger om tecknet.

Står det ett minustecken framför en parentes, så byts tecknen inuti parentesen vid multiplikation.

Vi tittar närmre på det i följande exempel

$$3-{\color{Blue} {2x}}\cdot ({\color{Red} {4+3x}})=$$

$$3-({\color{Blue}{ 2x}}\cdot {\color{Red} 4}+{\color{Blue} {2x}}\cdot {\color{Red} {3x}})=$$

$$3-(8x+6x^{2})$$

$$3-8x-6x^{2}$$

Om vi ska multiplicera ihop två parenteser, så ska varje term i den ena parentesen multipliceras med varje term i den andra parentesen. Detta ser vi nedan i fallet med två förstagradspolynom, innehållande vardera en variabelterm och en konstantterm, som ska multipliceras med varandra:

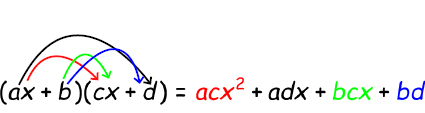
Ett exempel på detta kan se ut har vi här nedan (dessa polynom har två variabler, x och y, men sättet man räknar på är detsamma):

$$({\color{Red} {5x}}+2y)\cdot ({\color{Green} {3x}}+{\color{Blue} {4y}})=$$

$$={\color{Red} {5x}}\cdot {\color{Green}{ 3x}}+{\color{Red} {5x}}\cdot {\color{Blue} {4y}}+2y\cdot {\color{Green} {3x}}+2y\cdot {\color{Blue} {4y}}=$$

$$=15x^{2}+20xy+6xy+8y^{2}=$$

$$=15x^{2}+26xy+8y^{2}$$

Anledningen till att alla termer i det ena polynomet måste multipliceras med alla termer i det andra polynomet kan vi se illustrerat i figuren här nedan, där vi låter de båda polynomen representera rektangelns sidor och deras produkt representera rektangelns area:

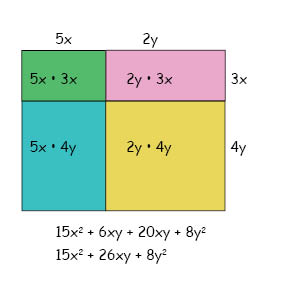
Produkten vi får fram när vi multiplicerar sidorna på rektangeln är alltså densamma som rektangelns area. Den hela rektangelns area består i sin tur av summan av de mindre rektanglarnas areor (märkta med grön, rosa, blå och gul färg i figuren) och dessa delareor bildar tillsammans den totala arean (produkten av de båda polynomen).

I det här avsnittet har vi bland annat gått igenom hur vi går till väga när vi ska multiplicera två polynom. Det finns några specialfall av multiplikation med polynom som är nyttiga att känna till, specialfall som vi nu ska gå igenom i avsnitten om kvadreringsreglerna och konjugatregeln.