Andragradsekvationer

I ett tidigare avsnitt gick vi igenom polynom och kom fram till att ett polynoms gradtal bestäms av den variabelterm som har störst exponent. Har ett polynom gradtalet 2, så kallar vi det ett andragradspolynom.

En ekvation vars ena led utgörs av ett andragradspolynom och vars andra led är lika med noll kallar vi en andragradsekvation. Det här är en mycket viktig typ av ekvation som förekommer i många olika sammanhang och därför ska vi ägna det här och efterföljande avsnitt åt att närmare undersöka just andragradsekvationer.

Andragradspolynom

Vi kan allmänt skriva ett polynom av andra graden på följande form:

$$ax^{2}+bx+c$$

där a, b och c är konstanter, och a ≠ 0 (om a = 0, så hade ju x²-termen blivit lika med noll och då hade inte polynomet varit av grad 2 längre, alltså inget andragradspolynom; däremot får b och/eller c vara lika med noll).

Ett exempel på ett andragradspolynom är

$$x^{2}+3x+1$$

där x² är den variabelterm som har störst exponent och därför avgör polynomets gradtal. I detta exempel har vi utifrån den allmänna formen ovan konstantvärdena a = 1, b = 3 och c = 1. (Som vanligt skriver vi inte ut 1 när ettan står framför ett x.)

Andragradsfunktioner

En andragradsfunktion är en funktion som kan skrivas på formen

$$f(x)=ax^{2}+bx+c$$

där a, b och c är konstanter, och a ≠ 0. Det är alltså en funktion, där själva funktionsuttrycket utgörs av ett andragradspolynom.

Utifrån vårt tidigare använda exempelpolynom ovan kan vi ha en andragradsfunktion som ser ut så här

$$f(x)=x^{2}+3x+1$$

Andragradsekvationer

Om vi har en ekvation på formen f(x) = 0, där f(x) är en andragradsfunktion enligt ovan, så kallar vi den typen av ekvation en andragradsekvation.

En andragradsekvation ska alltså gå att skriva på formen

$$ax^{2}+bx+c=0$$

där a, b och c är konstanter, och a ≠ 0.

Det är inte alltid så att en andragradsekvation som vi träffar på står i just denna form från början, men för att vara en andragradsekvation ska vi kunna skriva om den så att den står enligt den här formen. Till exempel förekommer det att det inte står 0 i det högra ledet, utan till exempel en konstantterm. I sådana situationer får vi då först subtrahera konstanttermen från båda leden, för att få det högra ledet lika med noll. Exakt vilka räkneoperationer vi behöver ta till för att få andragradsekvationen att stå på den önskade formen varierar från fall till fall.

Med vårt tidigare använda exempelpolynom kan en andragradsekvation skrivas som

$$x^{2}+3x+1=0$$

Att lösa en andragradsekvation innebär att vi hittar något eller några värden på den ingående variabeln sådana att f(x) = 0, det vill säga, sådana att polynomet blir lika med noll när vi sätter in värdet istället för variabeln.

Vi ska nu titta närmare på förhållandet mellan en andragradsekvation och motsvarande andragradsfunktion, och hur vi kan använda detta för att lösa andragradsekvationer och hitta särskilt intressanta variabelvärden då vi studerar en andragradsfunktion.

Andragradsfunktioners extrempunkter

Det enklaste andragradspolynomet är

$$x^{2}$$

vilket är det andragradspolynom vars konstantvärden utifrån den allmänna formen för andragradspolynom är a = 1, b = 0 och c = 0. Skriver vi ut dessa värden (vilket vi vanligtvis inte brukar göra) får vi följande:

$$ 1\cdot x^2+0\cdot x+0$$

Motsvarande andragradsfunktion är

$$f(x)=x^{2}$$

Om vi skissar denna andragradsfunktions graf i ett koordinatsystem, så ser vi att den ser ut så här:

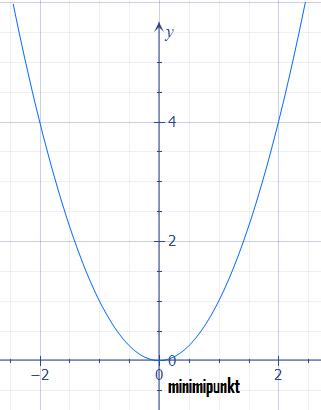
En funktion vars graf ser ut så här kallas för en parabel och är en ickelinjär funktion.

Funktionen antar sitt minsta funktionsvärde då x = 0. En punkt där funktionen antar sitt minsta värde i ett intervall kallas för en minimipunkt. När vi har en andragradsfunktion med en positiv koefficient framför x²-termen kommer funktionen alltid att ha en minimipunkt för något x-värde.

Om vi istället tittar på en andragradsfunktion som har en negativ koefficient framför x²-termen, som till exempel funktionen nedan som har koefficienten -1, men vi skriver det så här:

$$f(x)=-x^{2}$$

så ser vi att den ser ut så här om vi skissar dess graf i ett koordinatsystem:

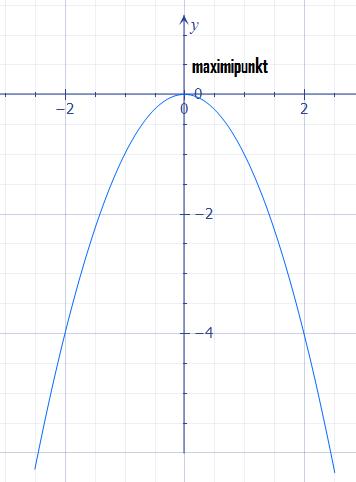
Här har funktionen sitt största värde då x = 0 och denna punkt där funktionen har sitt största värde i ett intervall kallas för en maximipunkt. En andragradsfunktion som har en negativ koefficient framför x²-termen har alltid en maximipunkt för något x-värde.

Ett samlingsnamn för maximi- och minimipunkter är extrempunkter. Om vi söker en funktions extrempunkter är det alltså dess maximi- och/eller minimipunkt(er) som vi letar efter.

I många sammanhang är vi intresserad av att hitta just det största eller minsta värdet som en funktion kan anta.

Det finns en enkel minnesregel för att komma ihåg om en andragradsfunktion har en minimipunkt eller en maximipunkt. En positiv koefficient framför x²-termen ger en skissad graf som liknar en glad (positiv) mun, som därför kommer att ha en minimipunkt. På motsvarande sätt gäller att en negativ koefficient framför x²-termen ger en skissad graf som liknar en ledsen (negativ) mun, varför dessa funktioner kommer att ha en maximipunkt.

Nollställen

Om vi istället skissar grafen till funktionen

$$f(x)=x^{2}+3x-4$$

så ser den ut ungefär så här:

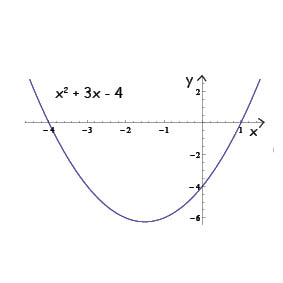
Vi ser att kurvan skär x-axeln i två punkter: där x = -4 och där x = 1.

Dessa två x-värden kallas för funktionens nollställen och är lösningar (även kallade rötter) till den motsvarande andragradsekvationen:

$$x^{2}+3x-4=0$$

Som vi kom fram till i början av det här avsnittet, är en andragradsekvation en ekvation som vi kan skriva på formen f(x) = 0, där f(x) är en andragradsfunktion. Dess lösningar är det värde eller de värden på variabeln som gör att andragradspolynomet blir lika med noll.

Vad vi har gjort här är helt enkelt att vi har skissat andragradsfunktionens graf och sedan letat rätt på de x-värden som gör att f(x) = 0, alltså för vilka x-värden som andragradsekvationens båda led ska vara lika med noll.

Att lösa en andragradsekvation på detta sätt, genom att skissa upp funktionens graf i ett koordinatsystem och sedan läsa av nollställena, kallas för att lösa ekvationen grafiskt.

En lösning till en andragradsekvation som ligger på den reella tallinjen kallas för en reell lösning. De båda x-värden som vi läste av i koordinatsystemet i exemplet, x = -4 och x = 1, är båda reella lösningar.

Antal lösningar

I avsnittsdelen ovan såg vi att andragradsekvationen

$$x^{2}+3x-4=0$$

har två reella lösningar eftersom kurvan till motsvarande funktion skär x-axeln två gånger (då x = -4 och då x = 1).

Tittar vi däremot på den enkla andragradsekvationen

$$x^{2}=0$$

så har denna ekvation bara en reell lösning, eftersom kurvan till dess motsvarande funktion, f(x) = x² bara skär x-axeln en gång (i minimipunkten, där x = 0):

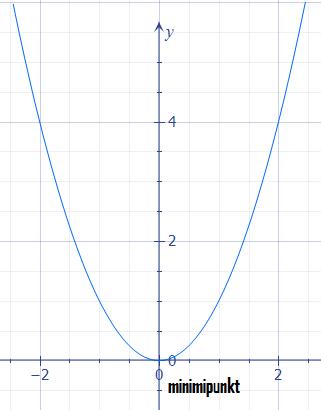
Har vi en andragradsfunktionen enligt följande

$$f(x)=x^{2}+2x+2$$

så har den en graf som ser ut ungefär så här:

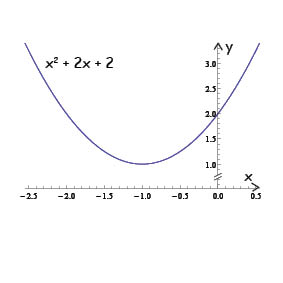
Som vi ser i koordinatsystemet, skär denna kurva aldrig x-axeln. Funktionen har sitt minimivärde då x = -1, så kurvan kommer aldrig att komma länge ner i y-led än denna punkt.

Försöker vi då att lösa andragradsekvationen

$$x^{2}+2x+2=0$$

grafiskt, så ser vi att eftersom andragradsfunktionen saknar nollställen, innebär detta i förlängningen också att ekvationen saknar reella lösningar. Att ekvationen saknar reella lösningar innebär att det inte finns några reella värden som vi kan tilldela variabeln så att ekvationens båda led blir lika med noll.

Vad vi nu har kommit fram till är de tre olika situationer som kan uppkomma då vi försöker att lösa en andragradsekvation:

Antingen har ekvationen två reella lösningar, en reell lösning eller också ingen reell lösning. Dessa situationer motsvarar att andragradsfunktionen har två nollställen, bara ett nollställe eller inget nollställe alls.

Symmetrilinje

En andragradsfunktion är alltid symmetrisk kring en symmetrilinje, vilket innebär att kurvan till vänster om symmetrilinjen är en exakt spegelbild av kurvan till höger om symmetrilinjen.

Ett exempel på detta är andragradsfunktionen y(x) = x², vars graf vi har skissat tidigare i det här avsnittet. Denna funktion är symmetrisk kring en symmetrilinje som sammanfaller med y-axeln (alltså där x = 0).

En andragradsfunktions symmetrilinje är alltid vertikal och parallell med y-axeln. En andragradsfunktions extrempunkt ligger dessutom alltid på symmetrilinjen. Den kommer alltid att ligga precis mittemellan eventuella nollställen som funktionen har. Det här är en användbar egenskap, för om vi känner till funktionens eventuella nollställen, då kan vi också räkna ut var symmetrilinjen ligger, vilket i sin tur identifierar funktionens extrempunkt.

Genom att räkna ut medelvärdet av nollställena så får vi alltså fram symmetrilinjen. Vi ska nu använda oss av denna egenskap för att identifiera extremvärdet för en funktion som vi stött på tidigare i det här avsnittet, nämligen

$$f(x)=x^{2}+3x-4$$

Som vi sett tidigare har denna funktion nollställen där x = -4 och där x = 1:

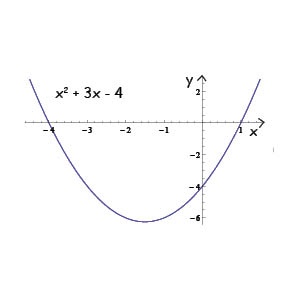
Eftersom vi vet att symmetrilinjen ska ligga mittemellan dessa båda nollställen, får vi att symmetrilinjens x-värde kan beräknas enligt

$$\frac{(-4)+1}{2}=\frac{-3}{2}=-1,5$$

Eftersom symmetrilinjen är vertikal definieras den helt av detta x-värde, x = -1,5. Funktionens extrempunkt ska ligga någonstans längs denna vertikala linje.

Ritar vi in symmetrilinjen i vårt koordinatsystem så ser vi att den hamnar mittemellan funktionens nollställen och skär kurvan i funktionens minimipunkt:

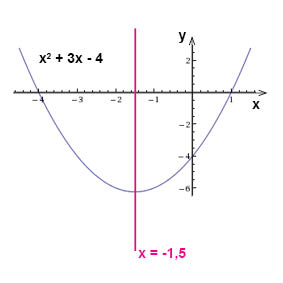
När vi nu har fått fram x-värdet för minimipunkten (detsamma som symmetrilinjens x-värde) kan vi genom att stoppa in detta värde i andragradsfunktion ta reda på motsvarande y-värde/funktionsvärde i denna punkt.

Vi får:

$$f(-1,5)=(-1,5)^{2}+3\cdot (-1,5)-4=-6,25$$

vilket gör att vi får minimipunktens koordinater till (-1,5; -6,25) och funktionens minimivärde till -6,25.