Funktionsbegreppet
I Matte 1-kursen gick vi igenom grunderna för koordinatsystem och i det förra avsnittet hur vi kan skissa grafer för att på så sätt tydliggöra samband. I det här avsnittet ska vi lära oss att använda det viktiga begreppet funktion och se hur dessa hänger ihop med grafer och koordinatsystem.
En funktion beskriver ett samband mellan två eller flera variabler.
Vi börjar med att titta på ett exempel på detta
Om Anna arbetar extra på helgerna, får hon en viss timlön då hon arbetar. Annas totala lön för det arbete hon utfört kan då ses som en funktion av antalet timmar som hon jobbat; ju fler timmar hon arbetat, desto mer kommer hon sammanlagt att ha tjänat.
Låt oss säga att Annas timlön är 80 kronor. För att beskriva hennes totala lön under en viss tidsperiod kan vi ställa upp följande funktion:
$$y=80x$$
där x är antalet timmar hon arbetat och y är den lön hon bör får ut efter att hon arbetat x antal timmar.
Ett till exempel på en funktion så kan vi beskriva vad som händer om vi släpper en boll från taket på en hög byggnad (där vi ignorerar luftmotståndet).
Vi beskriver bollens hastighet efter en viss tidpunkt med följande polynomfunktion:
$$v=9,81\cdot t$$
där hastigheten v (i meter per sekund) beräknas som 9,81 (tyngdaccelerationen) multiplicerat med tiden t (i sekunder, efter det att vi har släppt bollen); ju längre tid bollen har fallit, desto större hastighet kommer den att ha uppnått.
I detta exempel består polynomet i det högra ledet av en konstant (9,81) multiplicerad med en variabel (tiden t).
Med hjälp av polynomfunktionen ovan kan vi räkna ut bollens hastighet efter att 3,0 sekunder har gått efter att vi släppt bollen från taket. Det görs genom att ersätta t med 3,0:
$$v= 9,81 \cdot 3,0\approx 29 \text{ meter per sekund}$$
För varje värde på x finns det exakt ett värde på y, och det värdet beror på värdet av x - ändras värdet på x, så ändras också värdet på y. Därför kallas y för den beroende variabeln och x för den oberoende variabeln; värdet på variabeln y är beroende av vilket värdet är på x. I vårt exempel innebär detta helt enkelt att det för varje antal timmar Anna har arbetat finns en viss lön hon kommer att ha tjänat totalt.
En funktion är ett samband, en regel. Den kan liknas vid en maskin, där vi stoppar in ett värde, som vi till exempel kan kalla x, i den ena änden och får ut ett annat värde, som vi till exempel kan kalla y, i den andra änden. Det värde vi får ut, kallar vi funktionsvärdet.
För att visa att y verkligen beror av x (att y är den beroende variabeln) brukar vi skriva
$$y=f(x)$$
Detta utläses som att "f är en funktion av x", eller kort, "f av x". I vårt exempel med Annas lön skulle detta kunna skrivas så här:
$$f(x)=80x$$
Det vi tidigare har sett är beskrivning med hjälp av en formel som i fallet här ovanför med Annas lön som kunde beskrivas med funktionen
$$f(x)=80x$$
Vi kan också uttrycka funktionen med hjälp av ord. Vårt exempel blir då att funktionen för den totala lönen fås av att multiplicera timlönen, 80 kronor, med antalet timmar Anna arbetat.
Vi kan också beskriva funktionen med hjälp av en värdetabell:
| Antal timmar (x) | Total lön f(x) |
| 1 | 80 |
| 2 | 160 |
| 3 | 240 |
| 4 | 320 |
| 5 | 400 |
En funktion kan också beskrivas med hjälp av att funktionens graf åskådliggörs i ett koordinatsystem, som för vår funktion kan se ut så här:
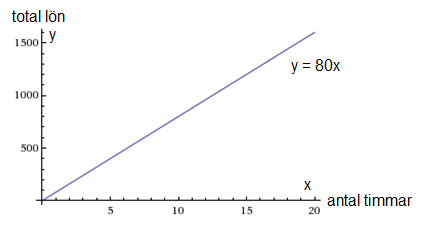
Lägg märke till att vi i koordinatsystemet ovan har olika gradering för x- och y-axlarna. Som vi nämnde i det förra avsnittet är det viktigt att välja en lämplig gradering på koordinataxlarna, så att sambandet vi vill visa tydligt framgår. I koordinatsystemet ovan gäller att varje steg längs x-axeln motsvarar en arbetad timme, medan varje steg längs y-axeln motsvarar 100 kr i lön.
Definitionsmängd och värdemängd
Om vi tittar vidare på funktionen som beskriver Annas lön, så ser vi att vi kan stoppa in negativa värden på x och få negativa y-värden (x = -1 ger till exempel y = -80), men vad skulle det betyda att Anna har arbetat ett negativt antal timmar? Kanske skulle vi kunna tolka det som att Anna blev skyldig 80 kronor för varje timme hon inte jobbar, men det blir konstigt, och så ser inte riktigt arbetsmarknaden ut idag och det är heller inte vad vi vill beskriva med vår funktion.
Vi kan konstatera att för att funktionen
$$y=80x$$
ska gälla för att beskriva Annas lön så som vi vill att den ska göra, så kan vi inte tillåta negativa värden på variabeln x. x-värdet måste alltså vara större än eller lika med 0. Anna kan inte heller inte jobba hur mycket som helst under en begränsad tid. Normalt arbetar vi inte mer än 40 timmar per vecka och det kan också vara så att Annas arbetsgivare inte tillåter henne att arbeta hur mycket som helst (dessutom har dygnet bara 24 timmar).
Det här betyder att det endast finns vissa värden på x där funktionen gäller - eller som det heter, där funktionen är definierad. Vi brukar kalla alla tillåtna x-värden för funktionens definitionsmängd; detta är den mängd av värden på den oberoende variabeln, i detta fall x, som är tillåtna.
I fallet med Annas lön, om vi tittar på en vecka, så kan definitionsmängden vara
$$0\leq x\leq 40$$
Vi tolkar denna definitionsmängd i det här sammanhanget som att Anna kan arbeta noll timmar eller mer, upp till maximalt 40 timmar, per vecka.
Varje tillåtet värde i x-led motsvarar ett specifikt värde i y-led. Alla möjliga värden på y kallas för funktionens värdemängd - värdemängden är de värden som funktionen kan anta.
I vårt exempel är definitionsmängden alla värden på x från 0 till och med 40, vilket motsvarar en värdemängd mellan 0 (om Anna arbetar 0 timmar, vilket ger lönen 80 ∙ 0 = 0 kronor) och 3200 (om hon arbetar 40 timmar, vilket ger lönen 80 ∙ 40 = 3200 kr).
Värdemängden kan vi därför skriva så här:
$$0\leq y\leq 3200$$
Här introducerar vi funktioner.
Här går vi igenom värdemängd och definitionsmängd.
Här går vi igenom hur vi kan beskriva en funktion med hjälp av en graf i ett koordinatsystem.
Här går vi igenom funktioner och hur vi kan presentera dem.
- Funktion: en funktion är något med regler som kopplar ihop ett instoppat värde med ett värde som kommer ut. Instoppade värdet kallas variabel och är ofta betecknat med x.
- Definitionsmängd: de värden som en variabel som ingår i ett funktionsuttryck får anta, om vi har funktionen \(f(x)\) så är det alla x-värden som vi får stoppa in i funktionen
- Värdemängd: de värden som funktioner kan anta utifrån definitionsmängden, så om vi har en funktion så är det vad för y-värden vi får i grafen. Ett exempel kan vara \(f(x) = x^2\), vi får stoppa in vilka x-värden som helst, men funktionsvärdet som kommer ut blir alltid positiva värden och därför är värdemängden \( \{y\geq 0\}\)
